- *Corresponding Author:
- Paravastu Venkata Kamala Kumari
Vignan Institute of Pharmaceutical Technology, Beside VSEZ, Duvvada, Visakhapatnam, Andhra Pradesh 530049, India
E-mail: kamalaparavastu@gmail.com
| Date of Received | 07 June 2020 |
| Date of Revision | 01 January 2021 |
| Date of Acceptance | 12 June 2021 |
| Indian J Pharm Sci 2021;83(3):575-583 |
This is an open access article distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 License, which allows others to remix, tweak, and build upon the work non-commercially, as long as the author is credited and the new creations are licensed under the identical terms
Abstract
Current research has been done to develop statistically and optimized immediate release tablets for eslicarbazepine. Nineteen formulations of eslicarbazepine acetate immediate release tablets are prepared by wet granulation. The three-dimensional Box-Behnken design at three levels (33) was developed to study how selected independent variables affect dependent responses. After the initial test, three independent items were selected as follows; polyvinylpyrrolidone (A), tapioca starch (B) and galbanum gum (C). Responses to measure were the time of disintegration (Y1) and in vitro drug release at 45 min (Y2). In accordance with the independent variables, three different levels were established as the lowest, highest and middle variables tested. The predicted formula formulated with the Box-Behnken statistical design consisted of polyvinylpyrrolidone, tapioca starch and galbanum gum at the optimum levels of 2.49, 2.77 and 3 respectively.
Keywords
Eslicarbazepine, polyvinylpyrrolidone, galbanum, Box-Behnken, anti-epilepsy
Organizing, conducting and interpreting test results by performing a small number of trials are achieved through experimental design. Independent variables if by chance variated, scientists use experimental design in the production of their product/process to demonstrate their knowledge of it. The design space is done using design concepts like Design of Experiments (DoE) through the introduction of easy-to-use software tools and the regulatory guidelines are encouraged. If many independent factors vary in a random way, then it is impossible to determine what influenced the outcome. The DoE anticipates easy-to-use techniques even though the features vary at a reasonable level[1]. There are many purposes for a DoE application: studies to identify the most influential factors affecting the product/process being studied; full or fractional designs for the measurement of factorial results; indepth response studies that are particularly helpful in optimization, mixture designs etc. Optimization is used to obtain a combination of factors related to the response and robustness is used as a final test before product release, to ensure that it stays within the specification. The primary goal of any experimental study is to find a relationship between independent variables (factors) and dependent variables (results, outcomes) within the experimental framework[2]. Factors such as ingredients level, material properties, independent variable processing parameters as well and dependent variables are product properties or parameters that reflect the dependable process performance.
The test (experimental) design, in general, is used to simultaneously study the effects of multiple independent variables (factors) on response variability; therefore, it is a multivariate analysis method[3]. A large number of objects can be learned by performing a small number of tests in a simple test design where the important object can be easily identified using a full factorial design. Response design varies in atleast three levels and a wide range of factors of different levels (using experimental designs) is used.
Quality by design (QbD) is a proposal for a pharmaceutical product development program that focuses on identifying product performance, optimizing and improving process efficiency under critical quality specifications[4]. Multivariate analysis with a small number of experiments can be easily done with Box-Behnken design (BBD) face response surface methodology (RSM) and D-optimal design. The model-equation is produced by BBD to understand the relationship between variable (independent) and quality (dependent) responses. BBD is an independent quadratic design in which the treatment combination is centered at the edges of the process area and in the center. BBD designs are rotatable (or close to rotating) and require three levels of each factor[5].
Eslicarbazepine ((S)-licarbazepine, (S)-10-hydroxycarbazepine), a compound with anti-epileptic properties is found in eslicarbazepine acetate and is also one of the most effective active oxcarbazepine metabolites after oral administration[6]. High plasma concentrations (tmax) are detected in 1-4 h. Plasma protein binding is low (<40 %). Eslicarbazepine acetate has a half-life of 13-20 h. Intestinal absorption of carbamazepine is slow and variable, possibly due to its slow dissolution in intestinal fluid. The concentration of peak serum is usually obtained between 4 and 8 h after oral administration of the tablets and the bioavailability of immediate release tablets is found to be in the order of 75-85 %.
Typical oral drug products, such as tablets and capsules, are designed to dispense active medication immediately after oral administration. In the development of generic drug products, no deliberate effort was made to change the rate of drug release rate. Immediate release products lead to faster drug absorption and the onset of associated pharmacodynamic effects[7]. In the case of prodrugs, the pharmacodynamic activity may slow down due to active drug conversion by hepatic or intestinal metabolism or by chemical hydrolysis. Alternatively, in typical oral products containing lipophilic drugs, drug absorption may be delayed due to a slow dissolution or selective absorption throughout the gastrointestinal (GI) tract, which also led to the delayed onset in time.
The pattern of drug release from modified-release (MR) dosage forms is deliberately altered from the conventional (immediate release) formulation of the dose to achieve the desired therapeutic goal or better patient compliance. The term MR drug product is used to describe products that change the duration and/ or rate of drug substance. Immediate release of drugs is appropriate for drugs with a long shelf life, high bioavailability, low clearance and a low elimination half-life. But the main requirement for immediate release of the drug is poor solubility and the action of drug[8].
Materials and Methods
Materials:
Eslicarbazepine acetate was received as a gift sample from Ami life sciences Pvt. Ltd. Croscarmellose sodium; polyvinylpyrrolidone (PVP) K30 was obtained from Yarrow Chem. Products, Mumbai, tapioca starch and maize starch were obtained from Surya min chem., magnesium stearate, talc was obtained from Molychem. Galbanum was obtained from a local retailer.
Methods:
Preparation of immediate release tablets: Nineteen different formulations using natural binders of eslicarbazepine acetate tablets were prepared using the ingredients by wet granulation technique as given in Table 1[9]. Croscarmellose sodium was used as a superdisintegrant, tapioca starch, maize starch and galbanum were used as natural additives and PVP was used as a synthetic binder. Magnesium stearate was used as a lubricant and talc as a glidant[10]. Various concentrations of 1 %, 2 % and 3 % were prepared by wet granulation technique using drug and excipients. The granules were passed through a number ≠ sieve no. 10 and then dried in hot air oven at 60°. The dried granules were passed through ≠ sieve no. 22 and were lubricated with magnesium stearate and talc. Eventually the dried granules were compressed as tablets with a MiniPress.
| Independent variables | Symbols | Levels | ||
|---|---|---|---|---|
| Lowest | Central | Highest | ||
| PVP | A | 1 | 2 | 3 |
| Tapioca starch | B | 1 | 2 | 3 |
| Galbanum gum | C | 1 | 2 | 3 |
| Constraints | ||||
| Dependent variables | Y1 | Minimize | ||
| Y2 | Minimize | |||
Table 1: Summarizes the Ranges and Constraints of Independent and Dependent Variables, Respectively
Drug content analysis:
A total of ten tablets were weighed and powdered. The powder equivalent to eslicarbazepine acetate was then dissolved in small amounts of methanol and made up to the required volume with distilled water[10]. The sample aliquot was then analyzed spectrophotometrically (Elite UV-150 double beam spectrophotometer) at 222 nm after serial dilution.
Disintegration time:
In the disintegration time study, the tablets were taken and placed in each tube of the disintegration apparatus in a 1 l beaker containing 900 ml of distilled water and the disintegration time was recorded at 37±2º.
In vitro dissolution studies:
United States Pharmacopeia (USP) dissolution test equipment (Model-DS 8000) type 2 (paddle) was used to carry the in vitro dissolution study. 900 ml of dissolution medium (0.1 N hydrochloric acid (HCl)) was taken in a basket and -0.75 % sodium lauryl sulfate (SLS) was added to the basket[11]. The temperature was maintained at 37±0.5°. The paddle speed was set at 50 rpm. The sample (5 ml) was filtered and diluted with 0.1 N HCl before being analyzed by UV Spectrophotometer (Elite UV-150 double beam spectrophotometer) at 222 nm.
Experimental design:
BBD at three levels (33) was developed to study how the selected independent variables influence dependent responses[12]. BBD was developed using the experimental version of Design-Expert® software 12. The design consisted of replicated center points and a group of points located in the center of each edge of a multidimensional cube that lowered the area of interest. The polynomial equation generated by this experimental design is given as follows:
Y0=b0+b1X1+b2X2+b3X3+b4X1X2+b5X2X3+b6X1X3 + b7X12+b8X22+b9X32
Where, Y0=dependent variable; X1, X2 and X3= independent variable coded levels; b0=intercept; b1 to b9=regression coefficients.
After preliminary experiments, three independent variables were chosen as follows; PVP (A), tapioca starch (B) and galbanum gum (C). The responses to be measured were disintegration time (Y1) and in vitro drug release at 45 min (Y2). Corresponding to the independent variables, three different levels were established as the lowest, the highest and central values of the tested variables (Table 1). The matrix of 19 experimental formulations was constructed as represented in Table 2.
| Factor 1 | Factor 2 | Factor 3 | Response 1 | Response 2 | |
|---|---|---|---|---|---|
| Run | A: PVP (mg) | B: Tapioca starch (mg) | C: Galbanum gum (mg) | Disintegration time (s) | In vitro drug release at 45 min (%) |
| 1 | 2 | 2 | 2 | 18 | 88.98 |
| 2 | 2 | 3 | 1 | 25 | 86.36 |
| 3 | 1 | 2 | 3 | 20 | 87.45 |
| 4 | 2 | 2 | 2 | 18 | 88.98 |
| 5 | 3 | 1 | 2 | 30 | 79.89 |
| 6 | 2 | 1 | 3 | 25 | 86.36 |
| 7 | 2 | 2 | 2 | 18 | 89.98 |
| 8 | 2 | 2 | 2 | 18 | 88.96 |
| 9 | 2 | 2 | 2 | 18 | 88.96 |
| 10 | 2 | 2 | 2 | 18 | 89.96 |
| 11 | 1 | 2 | 1 | 20 | 89.96 |
| 12 | 1 | 1 | 2 | 20 | 87.54 |
| 13 | 2 | 1 | 1 | 25 | 86.36 |
| 14 | 3 | 2 | 1 | 30 | 79.89 |
| 15 | 1 | 3 | 2 | 20 | 87.56 |
| 16 | 2 | 2 | 2 | 25 | 86.65 |
| 17 | 3 | 3 | 2 | 30 | 79.89 |
| 18 | 3 | 2 | 3 | 30 | 79.99 |
| 19 | 2 | 3 | 3 | 25 | 87.45 |
Table 2: Modeling of the Response in the Experimental Design
According to the suggested experimental design, 19 formulations (including 3 center points) were prepared experimentally in triplicate and characterized (Table 2). The obtained data were fitted to the appropriate models (linear, 2-FI and quadratic) and analyzed by the one-way analysis of variance (ANOVA). The models were explained by polynomial equations and their related three-dimensional (3D) response surface plots were created by design-expert® software[13]. For the purpose of model reduction and better predictability, the step-wise method was applied for the elimination of non-significant parameters. The main, interacting and quadratic effects of independent variables are (A, B and C), (AB, AC and BC) and (A2, B2 and C2) respectively.
| Dependent variables | p-value | Best fitted model | Lack of fit | Adequate precision | Predicted R2 | Adjusted R2 | R2 |
|---|---|---|---|---|---|---|---|
| Y1 (Disintegration time) | 0.0072 | Quadratic | Insignificant (p>0.05) | 5.7427 | 0.8027 | 0.7101 | 0.8550 |
| Y2 (in vitro drug release at 45 min) | <0.0001 | Quadratic | Insignificant (p>0.05) | 14.1521 | 0.8377 | 0.9323 | 0.9661 |
Table 3: Model Characteristics
The best significant fitted model was analyzed by ANOVA for the prediction of particle size as summarized in Table 3. This table demonstrates that the model is significant (p<0.05) whereas lack of fit is nonsignificant (p>0.05), which implies that the proposed model is adequate for prediction of the response[14,15]. The characteristics of the best-fitted model are summarized in Table 3. It could be observed from the table that the proposed quadratic model was significant (p<0.05) while lack of fit was non-significant (p>0.05), which connotes that the proposed model was appropriate for prediction of the response.
Optimization of formulation components:
Optimization process was carried out by relying on desirability measurement to get the levels of tested variables that could agree with the desirable responses[16,17]. Based on the required criteria, a suggestion was displayed with a desirability range from 0 to 1 where the desirability value towards 1 indicated the preference of response to its ideal value. Furthermore, the optimized formulation was determined and subjected to comparison of predicted and experimental values.
Results and Discussion
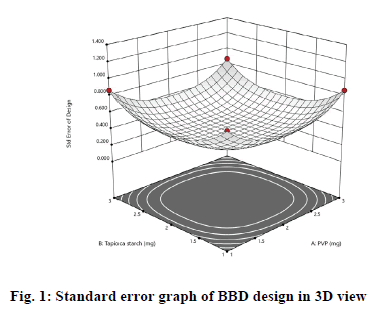
Statistical analysis of data was done. The validity of the utilized design was examined by standard error graph shown in fig. 1. This graph indicated the values of standard error of prediction for areas in the design space[18]. It was satisfactory to obtain relatively minimum values of standard error close to1or lower across the area of interest. The results revealed that the standard error was ranged between 0.378 and 0.866, hence implying the efficient potential of prediction of the design.
In the present study, ANOVA was applied at 95 % confidence level to evaluate the model significance. The model p-values observed for Y1 and Y2 responses were 0.0072 and <0.0001 respectively. This declared that the independent variables manifested significant effects on the tested responses away from experimental errors or chances. Besides, this illustration would be confirmed by greater values of F-ratio where their low values elucidated more error in the model. The rank order of the model predicting the capability of responses was determined as follow; Y2>Y1 which was based on small p-values and high values of F-ratios. In addition, lack of fit values could be used to inspect the efficiency of model taking into consideration of their p-values where non-significant values of lack of fit were good and fitted the satisfactory model[19]. The values of lack of fit for the observed dependent responses were 1.00 and 0.6314 with p-values of 0.0072 and <0.0001 for Y1 and Y2 respectively (Table 3). This concluded that lack of fit values was not significant and the chance for these large values due to noise was 0.72 % and 0.1 % respectively. Total 19 formulations were prepared for optimization of the 3 independent variables (A, B and C) and then characterized to analyze the influence exerted on the observed dependent responses (Y1 and Y2).
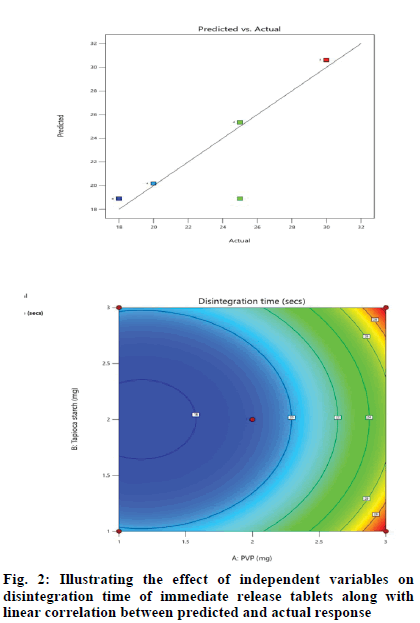
Effect of independent variables on disintegration time (Y1) was measured. Results mentioned in Table 3 showed the significance of the model because of the high F-ratio (5.90) with p-value of 0.0072. This revealed that the chance for this large F-ratio to occur due to noise is only 0.72 %. In our study, A, B, C, BC, A2 were significant terms owing to their significant p-values[20], otherwise, insignificant p-values greater than 0.1 were indicative for insignificant model terms. The predicted regression analysis (R2) of 0.8027 was in feasible agreement with the adjusted R2 of 0.7101 where the difference between them was less than 0.2. Also, adequate precision quantified the ratio of signal to noise. The desirable adequate precision of 5.7427 (greater than 4) indicated an adequate signal and the model could navigate the design space as shown in fig. 2.
The Model F-value of 5.90 implies the model is significant. There is only a 0.72 % chance that an F-value, this large could occur due to noise, p-values less than 0.0500 indicate model terms are significant. In this case A, B2, C2 are significant model terms. Values greater than 0.1000 indicate the model terms are not significant. If there are many insignificant model terms, model reduction may improve your model. The lack of fit F-value of 0.00 implies the lack of fit is not significant relative to the pure error. There is a 100.00 % chance that a lack of fit F-value this large could occur due to noise. Non-significant lack of fit is good.
The polynomial equation attained for this model was:
Y1=0.0533-0.0083*A-0.0050*A2-0.0067*B2- 0.0067*C2
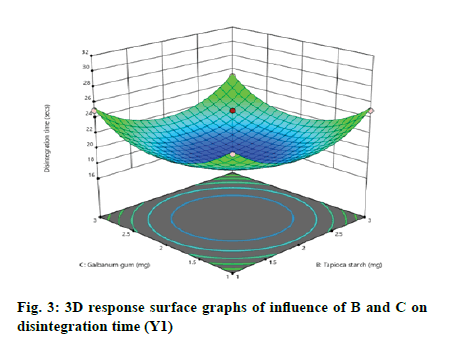
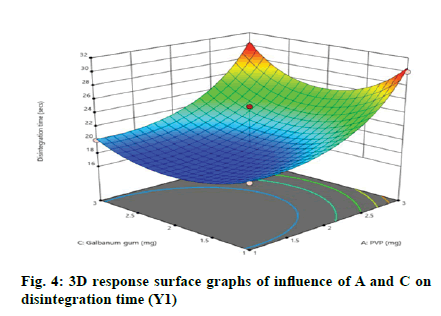
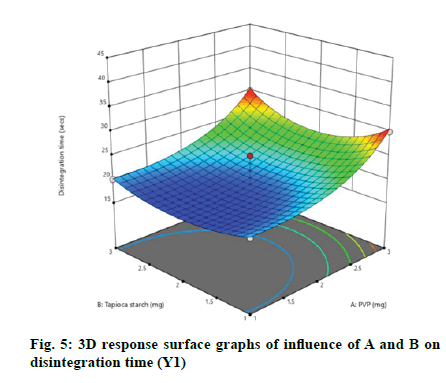
According to the regression equation, the positive sign in the equation indicates synergistic effects and the negative sign means antagonistic effects on the studied response. This equation stated that the variables have lesser impact on disintegration time[21,22]. The relationship between independent and dependent variables on disintegration time was studied by plotting the 3D response surface graphs (fig. 3, fig. 4 and fig. 5).
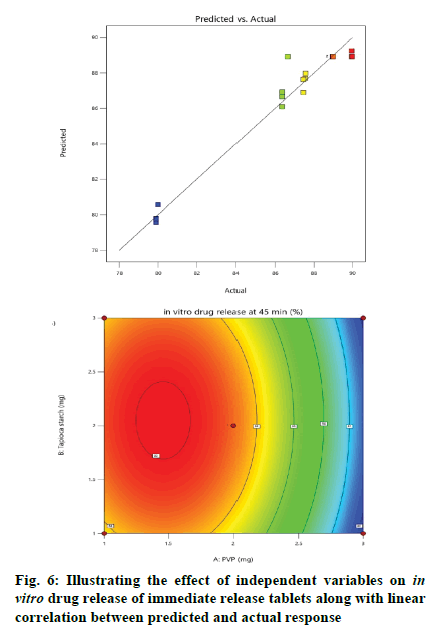
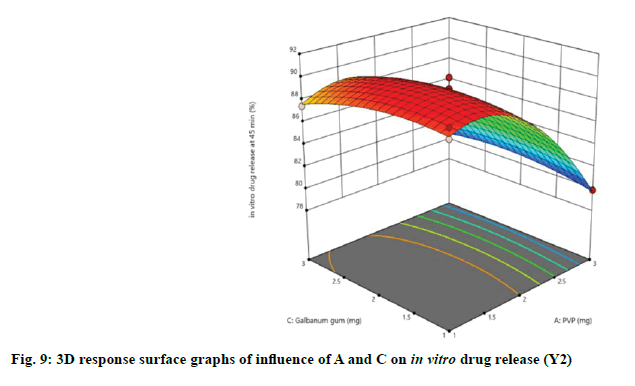
Effect of independent variables on in vitro drug release at 45 min (Y2) was measured. As presented by Table 3, the high F-ratio of 28.53 with p-value of <0.0001 implied that the model was significant and there was only a 0.01 % chance that this F-ratio occurred due to noise. In this model, A, B, C, A2, B2, C2 were significant model terms because of their significant p-values, while other terms were not significant. Also, the predicted R2 (0.8377) was in reasonable agreement with the adjusted R2 (0.9323). The desirable adequate precision of 14.1521 pointed out that the model could express the design space. The effect of independent variables on in vitro drug release of immediate release tablets along with linear correlation between predicted and actual response was shown in fig. 6.
The polynomial equation was determined as follow: Y2=0.0112+0.0006*A-0.0001*AC+0.0005*A2+0.000 2*B2+0.0001C2
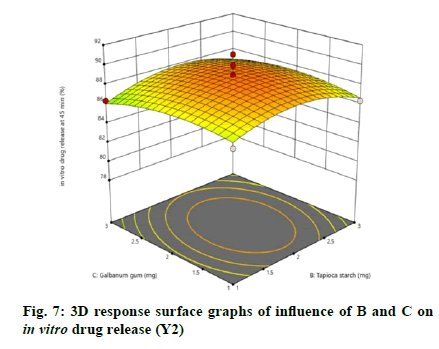
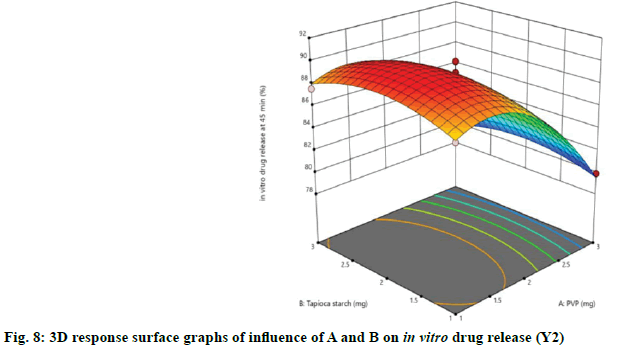
The relationship between independent and dependent variables on in vitro drug release at 45 min was studied by plotting the 3D response surface graphs (fig. 7, fig. 8 and fig. 9).
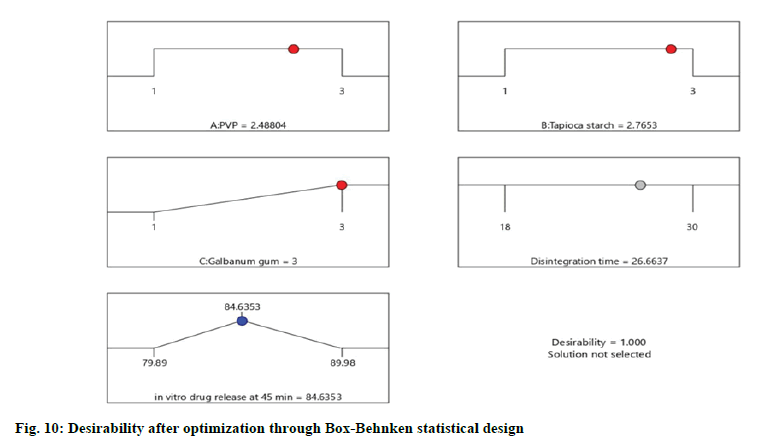
The optimized formulation with maximum desirability were prepared and evaluated for the validation of model. The result of predicted and observed response for the optimized formulation of immediate release tablets with maximum desirability are shown in Table 4.
| Response | Predicted mean | Predicted median* | Observed |
|---|---|---|---|
| Disintegration time | 27.1005 | 26.6637 | 23.00 |
| in vitro drug release | 84.646 | 84.6353 | 86.37 |
Table 4: Predicted and Observed Responses of Formulation Composition with Maximum Desirability Suggested Box-Behnken Statistical Design
Table 4 predicted and observed responses of formulation composition with maximum desirability suggested Box-Behnken statistical design.
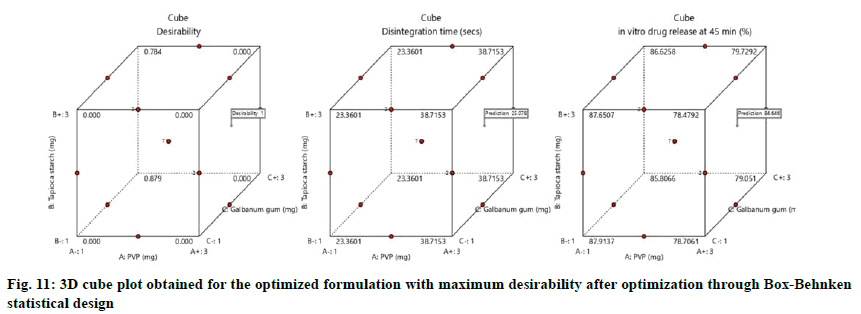
The values were in goodness of agreement. This is providing confirmation for the productive design validity and optimization. The desirability values of the numerical optimization process are shown in fig. 10 and fig. 11.
The optimized formula predicted for the optimized formulation of eslicarbazepine immediate release tablets through Box-Behnken statistical design consisted of PVP, tapioca starch and galbanum gum at optimum level of 2.49, 2.77 and 3 respectively.
With the help of BBD, three factors at three levels (33) were selected to study how the independent variables influence the dependent responses after preparation of immediate release tablets of eslicarbazepine. After preliminary experiments, three independent variables were chosen as follows; PVP (A), tapioca starch (B) and galbanum gum (C). The responses to be measured were disintegration time (Y1) and in vitro drug release at 45 min (Y2). Corresponding to the independent variables, three different levels were established as the lowest, the highest and central values of the tested variables. The matrix of nineteen experimental formulations was constructed. Standard error graph was satisfactory to obtain relatively minimum values of standard error close to1or lower across the area of interest. The optimized formula predicted for the optimized formulation of eslicarbazepine immediate release tablets through Box-Behnken statistical design consisted of PVP, tapioca starch and galbanum gum at optimum level of 2.49, 2.77 and 3 respectively.
Funding:
No financial funding.
Conflicts of interest:
The authors declared no conflict of interest.
References
- Politis SN, Colombo P, Colombo G, Rekkas DM. Design of experiments (DoE) in pharmaceutical development. Drug Dev Ind Pharm 2017;43(6):889-901.
- Bezerra MA, Santelli RE, Oliveira EP, Villar LS, Escaleira LA. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008;76(5):965-77.
- Kamala Kumari PV, Sankar GG, Prabhakar T. Strain improvement studies for the production of L-asparaginase by Beauveria bassiana SS18/41. Int J Pharm Sci Res 2015;31(2):173-6.
- Zhang L, Mao S. Application of quality by design in the current drug development. Asian J Pharm Sci 2017;12(1):1-8.
- Sangshetti JN, Deshpande M, Zaheer Z, Shinde DB, Arote R. Quality by design approach: Regulatory need. Arab J Chem 2017;10:S3412-25.
- Candioti LV, De Zan MM, Camara MS, Goicoechea HC. Experimental design and multiple response optimization. Using the desirability function in analytical methods development. Talanta 2014;124:123-38.
- Singh RP, Asconape JJ. A review of eslicarbazepine acetate for the adjunctive treatment of partial-onset epilepsy. J Cent Nerv Syst Dis 2011;3:S4888.
- Nyol S, Gupta MM. Immediate drug release dosage form: A review. J Drug Deliv Ther 2013;3(2).
- Schreiner T, Schaefer UF, Loth H. Immediate drug release from solid oral dosage forms. J Pharm Sci 2005;94(1):120-33.
- Rai VK, Pathak N, Bhaskar R, Nandi BC, Dey S, Tyagi LK. Optimization of immediate release tablet of raloxifene hydrochloride by wet granulation methodInt J Pharm Sci Res 2009;1(1):51-4.
- Agarwal S, Kamala Kumari PV, Rao YS. Formulation, evaluation and comparision of dissolution profiles of Eslicarbazepine acetate immediate release tablets using natural binders against synthetic binder. Int J Pharm Pharm Sci 2013;5(4):192-4.
- Demirturk E, Levent ON. Evaluation of in vitro dissolution profile comparison methods of immediate release gliclazide tablet formulations. Hacettepe Univ Eczacı Fak Derg 2005(1):1-10.
- Rath S, Gupta BK, Bala NN, Dhal HC. Formulation and optimization of immediate release telmisartan tablets using full factorial design. Int J App Pharm 2011;3(3):587-610.
- Abd Elbary A, Aboelwafa AA, Al Sharabi IM. Once daily, high-dose mesalazine controlled-release tablet for colonic delivery: optimization of formulation variables using Box–Behnken design. AAPS PharmSciTech 2011;12(4):1454-64.
- Lawrence XY, Amidon G, Khan MA, Hoag SW, Polli J, Raju GK, et al. Understanding pharmaceutical quality by design. AAPS J 2014;16(4):771-83.
- Kumari KP, Shankar GG, Prabhakar T. Optimisation of L-asparaginase production by Streptomyces griseoluteus WS3/1 using experimental methods. J Pharm Biochem Sci 2011;10(11):1-6.
- Ibrahim TM, El-Megrab NA, El-Nahas HM. Optimization of injectable PLGA in-situ forming implants of anti-psychotic risperidone via Box-Behnken design. J Drug Deliv Sci Technol 2020;58:101803.
- Ismail S, Khattab A. Optimization of proniosomal itraconazole formulation using Box Behken design to enhance oral bioavailability. J Drug Deliv Sci Technol 2018;45:142-50.
- Xie H, Gan Y, Ma S, Gan L, Chen Q. Optimization and evaluation of time-dependent tablets comprising an immediate and sustained release profile using artificial neural network. Drug Dev Ind Pharm 2008;34(4):363-72.
- Tak JW, Gupta B, Thapa RK, Woo KB, Kim SY, Go TG, et al. Preparation and optimization of immediate release/sustained release bilayered tablets of loxoprofen using Box–Behnken design. AAPS PharmSciTech 2017;18(4):1125-34.
- Abedullahh MH. Box-behnken design for development and optimization of acetazolamide microspheres. Int J Pharm Sci Res 2014;5:1228-39.
- Romero DC, Lourenço FR. Measurement uncertainty of dissolution test of acetaminophen immediate release tablets using Monte Carlo simulations. Braz J Pharm Sci 2017;53(3).