- *Corresponding Author:
- Hoda Khosravi
Department of Software Engineering, Islamic Azad University Sari branch, Mazandaran, Iran
E-mail: hoda_khosravi@ymail.com
| This article was originally published in a special issue, “Recent Trends in Biomedical Research” |
| Indian J Pharm Sci 2020:82(1)spl issue1; 91-97 |
This is an open access article distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 License, which allows others to remix, tweak, and build upon the work non-commercially, as long as the author is credited and the new creations are licensed under the identical terms
Abstract
Given the increasing need for the creation and development of automated systems, the problem of detecting and identifying the faces of people in the images has been considered by the researchers. In recent years, the sparse representation based classification has been of great interest to researchers. The goal of this investigation is to provide a quick and effective way to identify faces based on the sparse representation. Since the basis of sparse representation is to calculate it through L1-norm optimization for high dimensional dictionary with high computational volume, a smoothed L0-norm optimization-based method was introduced. At the time of obtaining the sparse representation using smoothed L0-norm, due to the high degree of redundancy, when the number of facial features is low, the conditions for the unique sparse representation are not properly satisfied or the model is not accurate, the risk of getting stuck in the local minima will be so much. Hence, the idea of the weighted sparse representation to narrow the search space is presented. In addition, to enhance the identification accuracy in face recognition and face verification under varying illumination conditions, the Singular Value Decomposition method can be used in the feature extraction step. In the extraction stage, the normalized coefficients of Singular Value Decomposition are not sensitive to different lightness conditions, resulting to reduce the effect of illumination variation on the normalized images. Compared to earlier methods, which often fail even in the event of a slight turbulence, this technique can successfully produce facial structural information while preventing the effect of different lightnesses such as cast shadows. The simulation results on the Extended Yale B database show that the proposed method has high accuracy in face recognition with less computational volume and higher speed than the L1-norm based approach.
Keywords
Face recognition, face subspace, sparse representation, smoothed L0-norm, L1- norm, weighted L0-norm, SVD face
Over the past 20 y, face recognition has drawn the attention of many researchers in various fields, such as security, psychology and engineering. On the other hand, with the advancement of technology, interactions between humans and computers will also increase. One of the key steps in this interaction is face recognition [1]. Face recognition is one of the important tools for identification in the field of biometrics and various algorithms have been proposed in relation to it. Although most of these have experienced significant advances in various applications and research areas, they still face major challenges such as lightness, gesture, expression and occlusion. There are a lot of ways in this area, but one important point that should always be considered is which feature contains very important information for identification? According to the geometry and appearance of the face, where fixed filter banks such as down sampling, Fourier, wavelet and Gabor are not used, which are suitable tools for the analysis of static signals like texture, but instead methods that adaptively extract the facial features based on the given pictures (e.g. Eigen face [2], Fisher faces [3] and Laplacian faces [4]) are used (figure. 1). The face recognition can be performed by using these features and designing a classifier such as the nearest-neighbor (NN), the nearest-subspace (NS) or SVM. Considering the process of designing the face recognition algorithm, it is seen that the performance of the algorithm is dependent on 2 parts, the feature selection and classifier selection. In other words, if a feature is properly selected, then a simple classifier can perform well or a classifier with the simplest features can have a very good performance. Wright et al. proposed the sparse representation based classification (SRC) method [5] to obtain the minimum reconstruction error in classifier-based algorithms such as NN and NS. Particularly in the case of partial occlusion in facial images, the performance of their proposed method is better than NN and NS. In the first step, all training images are used to calculate the sparse representation (SR) coefficients of the test image. Then, the reconstruction errors between the test images and representation of each class are obtained. Finally, the test image is assigned to the class label that has the least amount of residual in the reconstruction errors. The results of the test show that SRC will provide excellent performance especially with respect to occlusion and resistance against noisy environments.
Figure 1: Original facial images and Eigenfaces, Laplacianfaces, down-sampled (12*10) and Random faces
a) Original facial images, b) 120-D representation in terms of four different features (left to right): Eigenfaces, Laplacianfaces, down-sampled (12*10) and Random faces [5]
In this paper, the singular value decomposition (SVD) face is used in the preprocessing stage. This method can properly extract significant and structural components of the face, such as eyes and mouth, under illumination variations, resulting in more precision in face recognition [6]. In this work, the SR approach was used to classify the extracted features. This method has a better performance than other classification ones. One of the most important features of this approach in comparison with other ones is it’s robustness against the fading of a part of the face. In this method, the L1-norm optimization, linear programming or basis pursuit (BP) are used to find the solution. Then, to minimize the computational complexity and execution time of the program, the smoothed L0-norm optimization (SL0), which has a higher convergence rate than BP, is used instead of the BP algorithm. If the uniqueness conditions are correctly met, SL0 algorithm is superior to BP algorithm in both terms of performance and speed [7]. As seen in the simulations, the SL0 algorithm did not properly converge due to the inaccuracy of the SR model or the presence of noise. Therefore, in order to solve this problem, the combination of NS and sparse representation classifiers was proposed based on weighted L0-norm. Firstly, the concepts of SVD face and SRC are expressed. Secondly, the weighted L0-norm is discussed along with the combined model of SR and NS classifiers and finally the simulation results were discussed.
Lightness normalization is a significant task in various areas of image processing, such as image registration, stereo vision, and object detection [6]. Recently, one of its most important applications has been the face recognition under various lightness conditions. However, changing the facial lightness often leads to some undesirable problems. For example, the spurious edges caused by shadows are confused with the true boundaries of facial components such as eyes or mouth. In SVD face, the dominant idea for solving this problem is to model the image I by multiplying the reflectance R and lightness L (I=R.L) [8]. The usefulness of the SVD-based design relies on the fact that the proposed design factorizes the distribution of local intensities and the corresponding coefficients (singular values) can probably reveal the lightness characteristics.
Accordingly, the SVD is applied to the local block B (x,y) containing N×N pixels, with the pixel position (x,y) in its center, B(x,y)=USVT, where U and V represent the orthogonal matrices UTU=I and VTV=I, respectively. The diagonal entries S = diag (λ1, ..., λn) refer to singular values of B (x,y). In the following, the largest singular value λ1 is normalized through the sum of the singular values as follows,  where λj represents the jth singular value. It is important to note that the normalized λ1 value is chosen as a feature, since this value denotes the dominant subspace energy. Figure. 2 shows some examples of the SVD faces. As can be seen, the proposed method will successfully maintain the facial underlying structures in different lightness conditions.
where λj represents the jth singular value. It is important to note that the normalized λ1 value is chosen as a feature, since this value denotes the dominant subspace energy. Figure. 2 shows some examples of the SVD faces. As can be seen, the proposed method will successfully maintain the facial underlying structures in different lightness conditions.
Figure 2: Some examples of SVD face
Note that the SVD face method always represents a same face under different lightness conditions (the leftmost image is the image taken under neutral light) [6]
It is important to emphasize that SVD face, even in the event of a sudden change in lightness conditions, has still a very good performance (columns 3 and 4 of figure. 2). The summary of the SVD face algorithm is as follows, for (x,y)=(1,1) to (W,H) do, where W and H are width and height of the image; *SVD conducted on each pixel position using the neighbor region B(x,y) of N×N pixels: B(x,y)=USVT, where S=diag(λ1, λ2…… λN); *conduct the relaxation of singular values: λj=λj+, *the largest singular value is normalized as follows,  , End for (SVD face:scale SF(x,y) values from 0 to 225)/(algorithm 1:SVD face (6).
, End for (SVD face:scale SF(x,y) values from 0 to 225)/(algorithm 1:SVD face (6).
The fundamental issue in identifying an object is to determine the test data class using labeled training samples of k distinct classes. ni training samples of i-th class are placed in columns of the matrix, Ai=[Vi,1,Vi,2,……Vi,n]×Rm×ni,…., in the face recognition, a black and white image with a dimension of w×h is represented through the vector R by sequentially placing the image columns. The columns of Ai denote the training facial images related to i-th person.
A variety of models and representations have been presented for Ai. According to one of the simplest and most effective models, every image or feature extracted from a class belongs to a linear subspace. Based on another model called as face subspace, the same facial images under lightness changes cover the approximate subspace with a low dimension in space Rm [2,9], i.e. each image class occupies a small part of the m-dimensional space. For simplicity, it is assumed that the training samples of each class form a subspace. Hence, each test vector sample y∈R m of i-th class can be approximated as a linear combination of the training sample vectors of i-th class with scalar values a i, j∈R, j=1,....m: y = ai,1vi,1+ai,2vi,2+….+ai,n vi,ni (Eqn. 2).
Since the test sample belonging to i-th class is not clear, the matrix A could be defined by putting in sequential order the matrices Ai, which is as follows, Eqn. 3, A = [A1, A2,….A]k ? R m×n. Therefore, the linear representation of the test vector sample y∈Rm is rewritten as follows, Eqn. 4, y=A0x ? Rm, where x0 =[0,…0,…,a i,1,…..a i,n,0,…,0]T is the coefficients vector. All entries of the coefficients vector are zero except for i-th class. Since entries of the vector x specify the identity of the test sample y, the solution of the linear Eqn y=Ax is important. Compared to local NS and NN methods, the methodology used here is global. It is clear that the solution of the linear equation y=Ax depends on the ratio of the number of equations m to the number of unknowns n. if m >n, then the linear equation y=Ax will be overdetermined and the unique solution can be found. For face recognition, the equation y=Ax is usually underdetermined (m<n) and then the solution is not unique. To solve this problem, the L2-norm solution is used which is as follows, Eqn. 5, 
Although the optimization of this problem can be simply solved by quasi-inverse matrix A, but because the solution is not sparse (in general), this solution does not contain specific information for the face recognition application. Considering the nature of the problem and concept of the face subspace model, SR techniques are suggested to solve this problem. Each very sparse solution can identify the identity of the test sample Y according to the stated concepts. Hence, the method for finding the sparsest solution of Eqn. y=Ax by solving the following optimization problem is proposed. Eqn. 6,  denotes the L0-norm and counts the number of non-zero entries. It is shown that if the matrix A is random and the Eqn. y=Ax has the answer that the number of its non-zero elements is less than half the number of Eqns m /2, this answer is unique, i.e.
denotes the L0-norm and counts the number of non-zero entries. It is shown that if the matrix A is random and the Eqn. y=Ax has the answer that the number of its non-zero elements is less than half the number of Eqns m /2, this answer is unique, i.e. ![]() [10]
[10]
The general theorem of uniqueness of sparse solution is expressed by the definition of the spark of the matrix A. The problem of finding the sparsest answer is a hard problem because L0-norm is not derivable. Several approximate approaches have been presented to solve this problem. In the following, we summarize the two methods proposed to solve this problem.
Materials and Methods
Finding the sparse solution by L1-norm minimization:
Many methods of solving (6) using the cost function, which is a measure of response sparseness, try to find the sparsest answer by solving an optimization problem. If the selected cost function is a better criterion for being sparse the vector x, then the accuracy of the final solution is higher. On the other hand, the desirable cost function is a function that simplifies the solving of the optimization problem. Some methods use the L1-norm minimization metric to measure the vector sparsity, namely: Eqn. 7,  .
.
Substituting of L0-norm with L1-norm converts the optimization problem into a convex one, which has appropriate methods (BP). It has been proven that in majority of underdetermined linear systems [11], L0-norm and L1-norm minimization leads to one solution, which is the sparsest one. Of course, in this method, the uniqueness condition is very limited compared to that of the answer (6). This is one of the reasons that some researchers have focused on ideas that directly solve the L0-norm problem. Researchers utilize the noise model [5] (7) for face recognition as follows: Eqn. 8,  in ||x||1 s.t, y ||y - Ax||2 ≤ ε. Here the model y=Ax+z was used to represent the test sample, which z=R m includes the noise model with limited energy ||z||2 ≤ ε.
in ||x||1 s.t, y ||y - Ax||2 ≤ ε. Here the model y=Ax+z was used to represent the test sample, which z=R m includes the noise model with limited energy ||z||2 ≤ ε.
Finding the sparse solution by smoothed L0-norm minimization:
As shown below, the main idea of this method is to use a continuous and smooth function for the L0-norm approximation of the vector x, Eqn. 9, ||x||2≈m-Σexp (-x2i/2σ2)=m-Fσ(x), If σ tends to zero, the approximation sign is converted to equality. Therefore, maximizing the function Fσ (x) for a small σ is equivalent to minimizing the L0-norm. Therefore, the optimization problem will be as follows, Eqn. 10,  m axFσ(x) s.t,y=Ax. To find the answer to the above problem, we can use the steepest descent maximization algorithm. For details of the optimization algorithm of problem (10) called as SLO [7]. An important feature of this algorithm is the high convergence rate and its good performance compared with the BP algorithm.
m axFσ(x) s.t,y=Ax. To find the answer to the above problem, we can use the steepest descent maximization algorithm. For details of the optimization algorithm of problem (10) called as SLO [7]. An important feature of this algorithm is the high convergence rate and its good performance compared with the BP algorithm.
Classification based on sparse representation:
For the new test sample y associated with one of training set classes, firstly SR was obtained using (7) or (8) or (9). Ideally, non-zero entries in x0 estimation are related to i-th class columns. Therefore, the test sample y was assigned to that class. However, this is not the case due to model error and noise. In fact, small non-zero entries corresponding to other classes can also be found. Accordingly, many classifications can be designed for the identification area. In one of the easiest ways, the class with the largest non-zero entry is considered as the winner. Nevertheless, the method presented in literature [5] is a more logical and subjective one. This approach examines which linear combination of classes training samples with coefficients obtained from SR offers a better approximation of the test sample y.
For each class i, vector ![]() derived from xˆ 0 is a vector in which entries corresponding to classes other than i are set to zero. By this definition, the approximation of the test sample y using the training samples of i-th class is equal to
derived from xˆ 0 is a vector in which entries corresponding to classes other than i are set to zero. By this definition, the approximation of the test sample y using the training samples of i-th class is equal to ![]() . So the classification of y is based on the best approximation, that is, the class with the least estimation error is the winner one, Eqn. 11,
. So the classification of y is based on the best approximation, that is, the class with the least estimation error is the winner one, Eqn. 11, ![]() .
.
The classification algorithm is summarized in the following. SRC algorithm’s summary, 1. input- matrix of training samples A∈Rn×m and test sample y∈Rm. 2. normalizing the columns of matrix A. 3. obtaining SR for the test sample using (6) or (7) or (8). 4. calculating the estimation error for all classes by 
 and, 5. output: identifying y with mi inri (y).
and, 5. output: identifying y with mi inri (y).
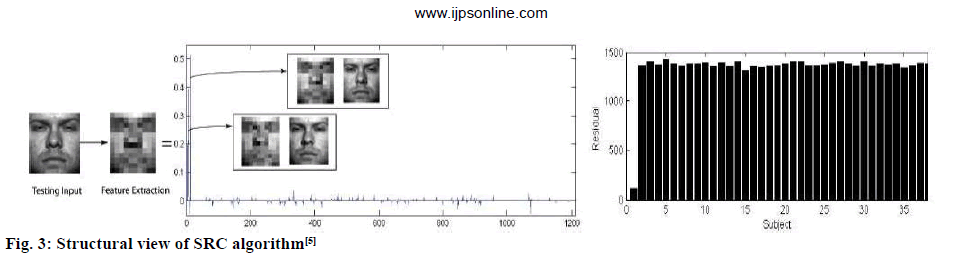
Figure. 3 briefly illustrates the steps involved in this algorithm. In this example, the down-sampled image is used as a feature, and the test image belongs to the first class. As shown in SR, the coefficients related to class 1 have a larger size. In this figure, images associated with two larger coefficients have also been shown in SR. These images correctly identified the person’s face. The diagram of sample to class 1. ri(y) also confirms this. ri(y) has the lowest value and assigns the test sample to class 1.
Figure 3: Structural view of SRC algorithm [5]
Weighted L0-norm and its application in sparse representation based pattern recognition:
The purpose of this section is to introduce a series of additional information into the problem of finding the sparse solution of the underdetermined equation system to improve the performance of the identification system.
As we will see in simulations, if uniqueness conditions are correctly satisfied, SL0 algorithm outperforms BP algorithm in terms of both performance and speed [7]. But in face recognition, it seems that the conditions are not correctly met, or that the algorithm gets stuck in the local minima and its classification performance degrades from the BP algorithm by 3-8 %. Given that one of the goals of this paper is to use the high speed of SL0 algorithm, in this section the weighted SR model was presented to solve the above-mentioned problem. First, we extract some preliminary information about the classification of the test sample by very simple algorithms such as NS and then use this information to optimize the algorithm SL0. In the following, weighted L0-norm and its application in pattern recognition are explained.
Weighted L0-norm [12]:
In the problems raised in the previous sections, the purpose of SR is to find the sparsest solution of underdetermined Eqn. Y=AX, which is mathematically equivalent to solving the following optimization problem, Eqn. 12,  where xi denotes i-th entry of vector x. In this problem, the probability of activity of all columns of A (activity of i-th column means large |xi|) is the same. Whether or not each column is active depends on the sample of the input signal and the column of the matrix A. There is no competition between the activity and non-activity and no external factor controls the activity of the columns in SR of the Y signal.
where xi denotes i-th entry of vector x. In this problem, the probability of activity of all columns of A (activity of i-th column means large |xi|) is the same. Whether or not each column is active depends on the sample of the input signal and the column of the matrix A. There is no competition between the activity and non-activity and no external factor controls the activity of the columns in SR of the Y signal.
Here, a strategy for controlling the probability of each column’s activity by weight has been provided. To this end, the optimization problem (12) was changed which is as follows, Eqn. 13,  , y=Ax, where Wi’s denote the controlling weight and are positive numbers. Here, the probability of activity of all columns in A is not the same, and Wi’s specify the probability of activity of the atoms. wi’s performance can be interpreted as follows, if wi is large, given the cost function (13), the probability of activity of i-th column is low and if wi is small, the probability of activity of i-th column is high. In other words, these weights limit the search space with respect to a series of previous information. In this way, one can control the activity of the columns in SR of the signal y by changing the wi’s. Problem (13) can be solved with simple modifications in the SL0 algorithm. The details of this algorithm are expressed in [12].
, y=Ax, where Wi’s denote the controlling weight and are positive numbers. Here, the probability of activity of all columns in A is not the same, and Wi’s specify the probability of activity of the atoms. wi’s performance can be interpreted as follows, if wi is large, given the cost function (13), the probability of activity of i-th column is low and if wi is small, the probability of activity of i-th column is high. In other words, these weights limit the search space with respect to a series of previous information. In this way, one can control the activity of the columns in SR of the signal y by changing the wi’s. Problem (13) can be solved with simple modifications in the SL0 algorithm. The details of this algorithm are expressed in [12].
Combination of SR classifier with weighted L0-norm:
According to the purpose of the paper, the reason for using the SL0 algorithm instead of the BP algorithm in the face recognition method is to increase speed [5]. But as could be seen in the simulations, this algorithm gets stuck in local minima due to some reasons such as the model’s lack of precision or the presence of noise. One way to solve this problem is to limit the search space of sparse solution of the algorithm, that is, to utilize the weighted L0-norm idea. Using the weighted L0-norm has a problem, how weights can be chosen? It seems that increasing speed would shift away from the goal. The solution provided is to use a very fast algorithm with very little computational volume as a preprocessing step. Here, it was suggested using the NS algorithm and a brief description is as follows.
NS classifier assigns the test sample y to i-th class, provided that distance from y to h-th class subspace created by the training samples Ai=[Vi,1,Vi,2,….,Vi,ni] ?Rm×ni has the lowest value compared with all classes. Eqn. 14,  . In other words, msei(y) represents the degree of similarity of the test sample y to i-th class. In this method, after calculating msei(y) with the help of the NS method, the vector of weight W is defined as the following, the entries corresponding to i-th class are set equal to msei(y). Then, the classification is performed by using (13) and the SR algorithm. This algorithm is called NSWSL0. Due to the use of optimization (13) as well as low computational volume of NS, the above-mentioned algorithm is an effective method in terms of computational volume and according to SL0 idea.
. In other words, msei(y) represents the degree of similarity of the test sample y to i-th class. In this method, after calculating msei(y) with the help of the NS method, the vector of weight W is defined as the following, the entries corresponding to i-th class are set equal to msei(y). Then, the classification is performed by using (13) and the SR algorithm. This algorithm is called NSWSL0. Due to the use of optimization (13) as well as low computational volume of NS, the above-mentioned algorithm is an effective method in terms of computational volume and according to SL0 idea.
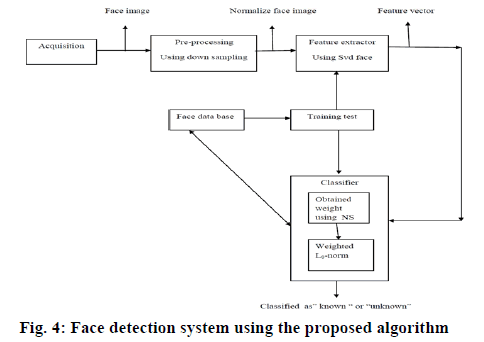
In the proposed method, chances of winning of classes in SR are controlled using the weights of the msei(y) determined by the NS. In other words, the initial and not very precise information obtained from the NS method is used to restrict the search space. As shown in simulations, when the number of features is low, this algorithm, while having high speed, has a performance similar to the BP method. In figure. 4, a face detection system is shown using the proposed algorithm.
Results and Discussion
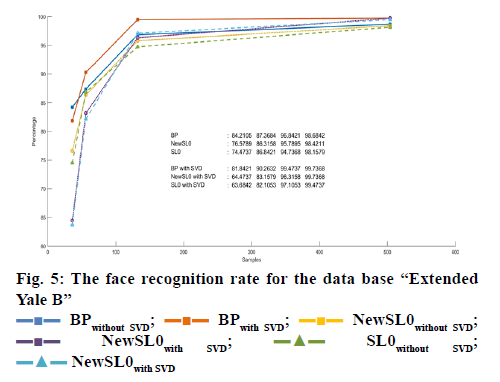
In this section, the performance of SRC was examined with features such as down sampling and SVD face. The database used is Extended Yale B. This database contains 2414 facial images from the front view of 38 people. All images have been taken with 192× 168 dimensions in different laboratory-controlled light conditions. For each class, 54 training files and 10 test files are randomly selected. Percent correct identification of the algorithm for the number of different features (36, 56,132 and 504) was calculated. These numbers are proportional to the down sampling ratios of 1/32, 1/24, 1/16 and 1/8, respectively. Also for SVD, N=7 (i.e. 7×7 pixels for B) and τ=10 was used. Here, the performance of SRC is computed for the algorithms BP, SLO, NSWSL0, BP+SVD, SL0+SVD and NSWSL0+SVD, and their results are compared. The test results are presented in figure. 5.
As shown in simulation results, the SVD and the combination of NS and SL0 based SR classifications have low computational power and high accuracy compared to the proposed algorithm in terms of BP [5], while whose performances are almost the same. NSWSL0+SVD, when the number of features is high, has the same performance as BP+SVD, but in each case it has a lower computational volume and a much higher speed, and its ideal identification rate is approximately 100 %. Table 1 shows the time spent by the CPU in seconds for face recognition algorithms. As the results show, the proposed algorithm has a lower consumption time than BP algorithm.
| Feature dimensions | ||||
|---|---|---|---|---|
| Feature dimensions | 36 | 56 | 132 | 504 |
| BP | 0.197 | 0.400 | 1.728 | 74.014 |
| SLO | 0.013 | 0.016 | 0.030 | 0.195 |
| NSWSL0 | 0.0419 | 0.0583 | 0.0954 | 0.353 |
| BP+SVD | 0.721 | 0.857 | 2.251 | 53.401 |
| SLO+SVD | 0.525 | 0.533 | 0.579 | 0.719 |
| NSWSL0+SVD | 0.540 | 0.551 | 0.586 | 0.762 |
Table 1: Time Spent By Cpu (Sec).
In this paper, in addition to the performance of the SVD face method for feature extraction and SRC in face recognition, the combined method of NS and SR classifiers using weighted L0-norm and SL0 has been investigated. In other words, the SL0 algorithm was sued to achieve high speed and precision in SRC and the combination of weighted L0-norm, SL0, NS simple classifier and feature extraction algorithm SVD face to achieve better classification performance.
NSWSL0+SVD, while enjoying high speed, have the same performance as the BP sparse representation classifier and also perform better when the number of features is high. Some of the works that can be done in the future are to improve the estimation of weighted L0-norm weights and use the different algorithms for feature extraction in terms of the challenges available to increase the performance of proposed methods.
Conflict of interest:
No conflict of interest between any of the authors.
References
- Liu X, Lu L, Shen Z, Lu K. A novel face recognition algorithm via weighted kernel sparse representation. Future Gener Comp Sy 2018;80:653-63.
- Turk MA, Pentland AP. Face recognition using eigenfaces. In Proceedings. Proc IEEE Comput Soc Conf Comput Vis Pattern Recognit 1991;3:586-91.
- Belhumeur PN, Hespanha JP, Kriegman DJ. Eigenfaces vs. fisherfaces: Recognition using class specific linear projection. IEEE Trans Pattern Anal Mach Intell 1997;7:711-20.
- He X, Yan S, Hu Y, Niyogi P, Zhang HJ. Face recognition using laplacianfaces. IEEE Trans Pattern Anal Mach Intell 2005;3:328-40.
- Wright J, Yang AY, Ganesh A, Sastry SS, Ma Y. Robust face recognition via sparse representation. IEEE Trans Pattern Anal Mach Intell 2008;3:210-27.
- Kim W, Suh S, Hwang W, Han JJ. SVD face: illumination-invariant face representation. IEEE Signal Process Lett 2014;21:1336-40.
- Mohimani H, Babaie-Zadeh M, Jutten C. A fast approach for over complete sparse decomposition based on smoothed norm. IEEE T Signal Proces 2008;57:289-301.
- Horn BK. Determining lightness from an image. Comput Graph Image process 1974; 3:277-99.
- Basri R, Jacobs DW. Lambertian reflectance and linear subspaces. IEEE Trans Pattern Anal Mach Intell 2003;1:218-33.
- Donoho DL, Elad M. Optimally sparse representation in general (nonorthogonal) dictionaries via ℓ1 minimization. Proc Natl Acad Sci 2003; 100:2197-202.
- Donoho DL. For most large underdetermined systems of linear equations the minimal ℓ1-norm solution is also the sparsest solution. Commun Pure Appl Math 2006;59:797-829.
- Ghaffari A, Babaie-Zadeh M, Jutten C. Sparse decomposition of two dimensional signals. In 2009 IEEE Int conf acoust speech signal process 2009;19:3157-160.


 BPwithout SVD;
BPwithout SVD;  BPwith SVD;
BPwith SVD;  NewSL0without SVD;
NewSL0without SVD;  NewSL0with SVD;
NewSL0with SVD;  SL0without SVD;
SL0without SVD;  NewSL0with SVD
NewSL0with SVD



