- Corresponding Author:
- P. Singh
Department of Chemistry, S.K. Government Post–Graduate College, Sikar–332 001, India
E-mail: psingh_sikar@rediffmail.com
| Date of Submission | 12 April 2012 |
| Date of Revision | 11 January 2013 |
| Date of Acceptance | 15 January 2013 |
| Indian J Pharm Sci 2013;75(1):36-44 |
Abstract
The tumour necrosis factor-α converting enzyme inhibition activity of a series comprising of novel tartrate-based analogues has been quantitatively analysed in terms of molecular descriptors. The statistically validated quantitative structure-activity relationship models provided rationales to explain the inhibition activity of these congeners. The descriptors identified through combinatorial protocol in multiple linear regression analysis have highlighted the role of Moran autocorrelation of lag 7, weighted by atomic van der Waals volume, presence of both prime and nonprime amide carbonyl oxygen in the tartrate moiety and occurrence of five membered ring bearing substituents at varying sites. A few potential novel tartrate-based analogues have been suggested for further investigation.
Keywords
Combinatorial protocol in multiple linear regression analysis, inhibitors of tumour necrosis factor?α converting enzyme, molecular descriptors, novel tartrate?based compounds, quantitative structure?activity relationship.
Tumour necrosis factor?α (TNF?α) is one of the cytokines, which is involved in immunomodulation and proinflammation events. The overproduction of TNF?α has been concerned in many autoimmune disorders namely rheumatoid arthritis, Crohn’s disease and psoriasis[1?4]. The reduction of TNF?α levels has been managed for successful treatment of inflammatory diseases[5]. Thus, the finding of a low cost, orally active small drug, which could moderate TNF?α levels is of prime importance at clinical level at present. One important strategy to reduce the levels of soluble TNF?α is to block the release of TNF?α from the cell surface by the inhibition of TNF?α converting enzyme (TACE)[6?8]. This enzyme being a membrane?bound zinc?metalloprotease is able to convert the 26?kD transmembrane pro?form of TNF?α to the mature 17?kD soluble form[9,10]. It has been shown that the active site of TACE shares many common features with the matrix metalloproteinases (MMPs)[11,12]. However, a unique feature of TACE is a tunnel interconnecting the S1′ and S3′ pockets into a single large cavity. The selectivity of TACE may be accomplished by incorporating appropriate substitutions that bind in the narrow S1′ tunnel and large S3′ pocket[13?17].
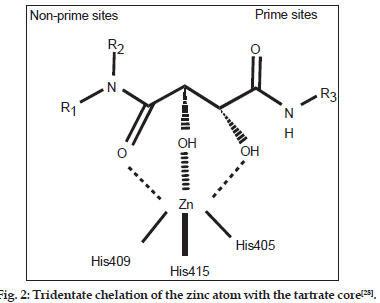
As the broad?spectrum MMP inhibitors exhibit a dose?limiting toxicity leading to side effects known as musculoskeletal syndrome (MMS)[18?25], therefore, selective inhibitors of TACE are desirable at present. As most of the common TACE inhibitors are hydroxamate based[26,27], the exploration of selective nonhydroxamate drugs, devoid of MMS, may be more potential TACE inhibitors. In view of this, Rosner, et al.[28] have screened their proprietary mixture?based combinatorial library with the automated ligand identification system[29?31] and were able to identify four compounds (Compound. 1?4; Table 1, fig. 1) of moderate TACE affinities. The structures of these compounds were similar to bis?amides of l?tartaric acid (tartrates)[32] while the corresponding d?tartrates were reported as inactive. This was the first report in which a unique tridentate zinc binding mode was revealed with the tartrate scaffold and is defined by the two hydroxyl groups and the nonprime amide carbonyl interacting with the catalytic zinc atom (fig. 2). The zinc atom maintains its coordination with the three imidazole nitrogen’s of His405, His409 and His415 and attains pseudo?octahedral coordination geometry during the binding mode. The prime amide carbonyl oxygen makes hydrogen bonds with the backbone –NH of both Leu348 and Gly349. The OH near the nonprime side also forms hydrogen bonds with the carboxylate oxygen of Glu406. In this way, all the four oxygen atoms on the tartrate core collectively make both the nonprime and prime binding interactions with the TACE protein. A novel series of compounds, able to undergo such interactions, were further prepared and evaluated for their binding affinity (Ki ) for TACE[28]. However this study, being sort of structure?activity relationship (SAR), was targeted at the alterations of substituents at different positions and provided no rationale to reduce the trial?and?error factors. Hence, the present communication is aimed at to perform a 2D quantitative structure?activity relationship (2D QSAR) for the reported compounds so as to provide the rationale for drug?design and to grasp some molecular features of the compounds for the property study relating to their binding affinity for TACE. In the congeneric series, where a relative study is being carried out, the 2D descriptors may play important role in deriving the significant relationships with biological activities of the compounds. The novelty and importance of a 2D?QSAR study is due to its simplicity for the calculations of different descriptors and their interpretation in physical sense. Thus the study may not fully explain the mode of interaction at the receptor site(s) but it will certainly reflect upon important molecular features relevant for the interaction.
| Compounds | R1 | R2 | nR05 | MATS7v | O-058 | pK (M) | ||
|---|---|---|---|---|---|---|---|---|
| Obsa | Calcd. Eq. 3 | Prtcd LOO | ||||||
| 1 | 3-Methoxy-4-piperazinyl | (2-Thiophen-2-ylethyl) amino | 1 | 0.048 | 2 | 6.4 | 6.15 | 6.12 |
| 2b | 2-Chlorophenyl-4-piperazinyl | (2-Thiophen-2-ylethyl) amino | 1 | 0.168 | 2 | 6.4 | 5.19 | - |
| 3 | 4-(Benzyl) piperidinyl | (2-Thiophen-2-ylethyl) amino | 1 | 0.051 | 2 | 5.96 | 6.12 | 6.14 |
| 4 | Cyclohexylmethylamino | (2-Thiophen-2-ylethyl) amino | 1 | 0.066 | 2 | 5.85 | 6 | 6.02 |
| 5 | 4-(2-Pyridinyl) piperazinyl | (2-Thiophen-2-ylethyl) amino | 1 | 0.14 | 2 | 5.6 | 5.41 | 5.37 |
| 6 | Dimethylamino | (2-Thiophen-2-ylethyl) amino | 1 | 0.131 | 2 | 5.89 | 5.49 | 5.39 |
| 7 | Benzylmethylamino | (2-Thiophen-2-ylethyl) amino | 1 | 0.034 | 2 | 6.12 | 6.26 | 6.27 |
| 8 | Methylphenethylamino | (2-Thiophen-2-ylethyl) amino | 1 | 0.054 | 2 | 5.89 | 6.1 | 6.12 |
| 9 | Furan-2-ylmethylmethylamino | (2-Thiophen-2-ylethyl) amino | 2 | 0.108 | 2 | 5.99 | 6.3 | 6.35 |
| 10 | Pyridine-3-ylmethylmethylamino | (2-Thiophen-2-ylethyl) amino | 1 | 0.015 | 2 | 6.03 | 6.41 | 6.46 |
| 11 | 2-Phenylpiperidinyl | (2-Thiophen-2-ylethyl) amino | 1 | 0.012 | 2 | 6.49 | 6.43 | 6.42 |
| 12 | 2-Phenylpyrrolidinyl | (2-Thiophen-2-ylethyl) amino | 2 | 0.04 | 2 | 7.02 | 6.84 | 6.83 |
| 13c | 3-Phenylpyrrolidinyl | (2-Thiophen-2-ylethyl) amino | 2 | 0.089 | 2 | 6.34 | 6.45 | - |
| 14c | 1,2,3,4-Tetrahydroisoquinolin-2-yl | (2-Thiophen-2-ylethyl) amino | 1 | 0.043 | 2 | 7.04 | 6.19 | - |
| 15 | 2,3-Dihydro-1H-isoindol-2-yl | (2-Thiophen-2-ylethyl) amino | 2 | 0.004 | 2 | 7.18 | 7.13 | 7.12 |
| 16c | 2-Pyridinyl-pyrrolidin-1-yl | (2-Thiophen-2-ylethyl) amino | 2 | 0.05 | 2 | 6.73 | 6.76 | - |
| 17 | 2-Thiazolyl-pyrrolidin-1-yl | (2-Thiophen-2-ylethyl) amino | 3 | 0.109 | 2 | 6.79 | 6.92 | 7.01 |
| 18 | 2-Chlorophenylpyrrolidin-1-yl | (2-Thiophen-2-ylethyl) amino | 2 | 0.048 | 2 | 6.49 | 6.78 | 6.8 |
| 19c | 3-Chlorophenylpyrrolidin-1-yl | (2-Thiophen-2-ylethyl) amino | 2 | −0.008 | 2 | 7.96 | 7.22 | - |
| 20 | 4-Chlorophenylpyrrolidin-1-yl | (2-Thiophen-2-ylethyl) amino | 2 | 0.077 | 2 | 6.12 | 6.55 | 6.58 |
| 21 | 3-Methylphenylpyrrolidin-1-yl | (2-Thiophen-2-ylethyl) amino | 2 | −0.049 | 2 | 7.89 | 7.55 | 7.48 |
| 22c | 3-Methoxyphenylpyrrolidin-1-yl | (2-Thiophen-2-ylethyl) amino | 2 | 0.041 | 2 | 7.48 | 6.83 | - |
| 23c | 3-Dimethylaminophenylpyrrolidin-1-yl | (2-Thiophen-2-ylethyl) amino | 2 | 0.043 | 2 | 7.39 | 6.82 | - |
| 24b | 3-Chlorophenylpyrrolidin-1-yl | Benzylamino | 1 | −0.050 | 2 | 5.84 | 6.92 | - |
| 25 | Phenylpyrrolidin-1-yl | (Benzofuran-2-ylmethyl) amino | 2 | 0.072 | 2 | 6.8 | 6.59 | 6.57 |
| 26 | Phenylpyrrolidin-1-yl | (4-Benzylthiophen-2-ylethyl) amino | 2 | 0.022 | 2 | 7.18 | 6.98 | 6.97 |
| 27 | 4-Fluorophenylpyrrolidin-1-yl | (4-Benzylthiophen-2-ylmethyl) amino | 2 | −0.029 | 2 | 7.03 | 7.39 | 7.44 |
| 28c | 3-Clorophenylpyrrolidin-1-yl | (4-Benzylbenzyl) amino | 1 | −0.021 | 2 | 7.15 | 6.69 | - |
| 29c | Phenylpyrrolidin-1-yl | (4-Benzylthiazol-2-ylethyl) amino | 2 | 0.031 | 2 | 7.32 | 6.91 | - |
| 30 | Phenylpyrrolidin-1-yl | (4-Benzylthiazol-2-ylmethyl) amino | 2 | −0.028 | 2 | 8.1 | 7.38 | 7.28 |
| 31 | Phenylpyrrolidin-1-yl | (4-Benzyloxazol-2-ylethyl) amino | 2 | 0.037 | 2 | 6.34 | 6.86 | 6.9 |
| 32 | Phenylpyrrolidin-1-yl | (4-Benzyloxazol-2-ylmethyl) amino | 2 | −0.006 | 2 | 7.66 | 7.21 | 7.16 |
| 33 | 3-Chlorophenylpyrrolidin-1-yl | [4-(2-Chlorobenzyl) thiophen-2-yl methyl] amino | 2 | −0.049 | 1 | 5.82 | 6.05 | 6.19 |
| 34 | 3-Chlorophenylpyrrolidin-1-yl | [4-(2-Chlorobenzyl) thiophen-2-yl methyl] amino | 2 | −0.052 | 1 | 5.95 | 6.07 | 6.15 |
| 35c | Thiazol-2-yl | (2-Thiophen-2-ylethyl) amino | 2 | 0.075 | 1 | 5.26 | 5.06 | - |
| 36 | 1-Methyl-1H-imidazol-2-yl | (2-Thiophen-2-ylethyl) amino | 2 | 0.131 | 1 | 4.97 | 4.62 | 4.22 |
| aTaken from Ref.[28], b‘Outlier’ compound, cTest-set compound, nR05=Number of five-membered rings, LOO=Leave-one-out | ||||||||
Table 1: Molecular descriptors, observed, calculated and predicted tumor necrosis factor-α converting enzyme inhibition activity of novel tartrate-based analogues.
Materials and Methods
The active compounds along with their binding constant, Ki under present investigation (Table 1) have been taken from the literature[28]. The generalised structure of these compounds is shown in fig. 1a and b. The binding affinity has been expressed on the negative logarithm as pKi (–logKi ) on the molar basis and stand as the dependent descriptor for present quantitative analysis. For modelling purpose, the data?set was divided into training? and test?sets to insure external validation of models derived through identified descriptors. Additionally, leave?one?out (LOO) and leave?five?out (L5O) procedures were employed for internal validation of generated models from the training?set.
The selection of compounds for test set has been made through SYSTAT, Systat Software Inc., Chicago, USA[33] using the single linkage hierarchical cluster procedure involving the Euclidean distances of the activity values. Nearly 25% of the compounds, from total population, were selected for this purpose. Based on the pKi values of the data set, a cluster tree was generated and compounds were selected in such a way to keep them at a maximum possible distance from each other. In this way, the test set includes the highest to lowest active congeners of the data set. In SYSTAT, by default, the normalised Euclidean distances are computed to join the objects of cluster. The normalised distances are root mean?squared distances. The single linkage uses distance between two closest members in clustering. It generates long clusters and provides scope to choose objects at different intervals. Due to this reason, a single linkage clustering procedure was applied.
Molecular descriptors
The structures of the compounds under study have been drawn in ChemDraw, Cambridge Soft Corporation, Cambridge, USA[34] using the standard procedure. These structures were converted into 3D objects using the default conversion procedure implemented in the CS Chem3D Ultra, Cambridge Soft Corporation, Cambridge, USA. The generated 3D?structures of the compounds were subjected to energy minimization in the MOPAC module, using the AM1 procedure for closed shell systems, implemented in the CS Chem3D Ultra. This will ensure a well?defined conformer relationship across the compounds of the study. All these energy minimised structures of respective compounds have been ported to DRAGON software (Virtual Computational Chemistry Laboratory, Munich, Germany)[35] for computing the descriptors corresponding to 0D, 1D, and 2D classes. Table 2 provides the definition and scope of these descriptor classes in addressing the structural features which were employed in present QSAR work. The combinatorial protocol in multiple linear regression (CP?MLR) computational procedure[36] has been used for present work in developing QSAR models. Prior to application of the CP?MLR procedure, all those descriptors which are intercorrelated beyond 0.90 and showing a correlation of less than 0.1 with the biological endpoints (descriptor vs. activity, r<0.1) were excluded. The remaining descriptors, able to address the biological activity of these compounds, will serve as the database (pool) at the end of this initial stage.
| Descriptor class (acronyms) | Definition and scope |
|---|---|
| Constitutional (CONST) | Dimensionless or 0D descriptors; independent from molecular connectivity and conformations |
| Topological (TOPO) | 2D-descriptor from molecular graphs and independent conformations |
| Molecular walk counts (MWC) | 2D-descriptors representing self-returning walks counts of different lengths |
| Modified Burden eigenvalues (BCUT) | 2D-descriptors representing positive and negative eigenvalues of the adjacency matrix, weights the diagonal elements and atoms |
| Galvez topological charge indices (GALVEZ) | 2D-descriptors representing the first 10 eigenvalues of corrected adjacency matrix |
| 2D-autocorrelations (2DAUTO | Molecular descriptors calculated from the molecular graphs by summing the products of atom weights of the terminal atoms of all the paths of the considered path length (the lag) |
| Functional groups (FUNC) | Molecular descriptors based on the counting of the chemical functional groups |
| Atom-centred fragments (ACF) | Molecular descriptors based on the counting of 120 atom-centred fragments, as defined by Ghose-Crippen |
| Empirical (EMP) | 1D-descriptors represent the counts of nonsingle bonds, hydrophilic groups and ratio of the number of aromatic bonds and total bonds in an H-depleted molecule |
| Properties (PROP) | 1D-descriptors representing molecular properties of a molecule |
Table 2: Descriptor classes used for the analysis of tumor necrosis factor-α converting enzyme activity of tartrae-based analogues and idenfified categories in modeling the activity.
Model development
The CP?MLR is a ‘filter’?based variable selection procedure for model development in QSAR studies[36]. Its procedural aspects and implementation are discussed in some of our recent publications[37?42]. The thrust of this procedure is in its embedded ‘filters’. They are briefly as follows: Filter?1 seeds the variables by way of limiting interparameter correlations to predefined level (upper limit ≤0.79); filter?2 controls the variables entry to a regression equation through t?values of coefficients (threshold value ≥2.0); filter?3 provides comparability of equations with different number of variables in terms of square root of adjusted multiple correlation coefficient of regression equation, r?bar; filter?4 estimates the consistency of the equation in terms of cross?validated r2 or q2 with LOO cross?validation as default option (threshold value 0.3≤q2≤1.0). All these filters make the variable selection process efficient and lead to a unique solution. In order to collect the descriptors with higher information content and explanatory power, the threshold of filter?3 was successively incremented with increasing number of descriptors (per equation) by considering the r?bar value of the preceding optimum model as the new threshold for next generation. Furthermore, in order to discover any chance correlations associated with the models recognized in CP?MLR, each cross?validated model has been put to a randomisation test[43,44] by repeated randomisation of the activity to discover the chance correlations, if any, associated with them. For this, every model has been subjected to 100 simulation runs with scrambled activity. The scrambled activity models with regression statistics better than or equal to that of the original activity model have been counted, to express the per cent chance correlation of the model under scrutiny.
| Descriptora | Avg. reg. coeff. (total incidence) b | Descriptora | Avg. reg. coeff. (total incidence) b |
|---|---|---|---|
| CONST | 2DAUTO | ||
| Me | −46.238 (1) | MATS4m | −54.517 (2) |
| RBN | −0.209 (1) | MATS6m | −56.186 (1) |
| nDB | 0.653 (2) | MATS8m | 58.640 (4) |
| nR05 | 0.634 (8) | MATS1v | 11.162 (2) |
| TOPO | MATS7v | −7.948 (10) | |
| MAXDN | 5.532 (7) | MATS4e | 8.109 (1) |
| PW3 | 42.594 (1) | MATS5e | 8.627 (1) |
| MWC | MATS1p | 9.324 (1) | |
| MWC09 | 7.772 (1) | FUN | |
| BCUT | nCs | −0.363 (2) | |
| BELm1 | 4.415 (1) | nNR2 | −0.762 (1) |
| BEHv1 | 4.960 (2) | ACF | |
| C-031 | 0.489 (1) | ||
| O-058 | 1.288 (13) | ||
| aThe descriptors are identified from the three-parameter models emerged fromCP-MLR protocol with filter-1 as 0.3, filter-2 as 2.0, filter-3 as 0.82, filter-4 as0.3≤q2≤1.0, and number of compounds in the study are 25 in the training-set andin the test-set, Me=The mean atomic Sanderson electronegativity (scaled on carbon atom), RBN=Number of rotatable bonds, nDB=Number of double bonds, nR05=Number of five-membered rings, MAXDN=Maximal electrotopologicalnegative variation, PW3=Path/walk 3-Randic shape index; MWC09=Molecular walkcount of order 9, BELm1 and BEHv1-Are the lowest and the highest eigenvalues no. 1 of Burden matrices/weighted, respectively, by atomic masses (m) and atomic van der Waals volumes (v), MATSkw=Moran autocorrelation, wherek and w represent, respectively, the lag and the atomic properties such as mass (m), van der Waals volume (v), Sanderson electronegativity (e) andpolarisability (p), nCs and nNR2=The number of total secondary C (sp3) andtertiary amines (aliphatic), respectively, C-031 and O-058, the functionalityX-CR–X and O=, respectively. bThe average regression coefficient of the descriptorcorresponding to all models and the total number of its incidences, the arithmeticsign of the coefficient represents the actual sign of the regression coefficient inthe models. CONST=Constitutional, TOPO=Topological, BCUT=Modified Burdeneigenvalues, 2DAUTO=2D-autocorrelations, ACF=Atom-centred fragments,FUN=Functional group |
|||
Table 3: Descriptors identified for modeling the tumor necrosis factor-α converting enzyme inhibition activity of tartrate-based analogues along with their average regression coefficients and the total.
Applicability domain
The utility of a QSAR model is based on its accurate prediction ability for new compounds. A model is valid only within its training domain and new compounds must be assessed as belonging to the domain before the model is applied. The applicability domain is assessed by the leverage values for each compound[45,46]. The Williams plot (the plot of standardised residuals versus leverage values, h) can then be used for an immediate and simple graphical detection of both the response outliers (Y?outliers) and structurally influential chemicals (X?outliers) in the model. In this plot, the applicability domain is established inside a squared area within ±x (standard deviation) and a leverage threshold h*. The threshold h* is generally fixed at 3(k+1)/n (n is the number of training?set compounds and k is the number of model parameters) whereas x=2 or 3. Prediction must be considered unreliable for compounds with a high leverage value (h>h*). On the other hand, when the leverage value of a compound is lower than the threshold value, the probability of accordance between predicted and observed values is as high as that for the training set compounds.
Results and Discussion
From the listed compounds in Table 1, two analogues (compound 2 and 24) have been removed from the study. The X?ray structure of compound 2 has revealed that the 2?chlorophenyl?piperazine group binds to the S1 subsite, defined by Val314, Lys315, Thr347 and Leu350. This subsite, being a flat hydrophobic patch, was solvent exposed. The chlorophenyl group appeared disordered and lacks 2fofc electron density[28]. The compound was unable to bind properly to the subsite and behave indifferently from other analogues of the series. Likewise, shortening of ethylene linker to the methylene linker resulted into significantly less active compound 24 compared to compound 21. Because of larger size of phenyl ring and shorter linker, the benzyl amide group of compound 24 may not able to bind properly in the narrow S1′ tunnel. This compound, therefore, also remained the ‘outlier’ of present study.
The remaining 34 compounds have been further divided into training and test sets. As mentioned above, the selection of test?set compounds was made through SYSTAT using the single linkage hierarchical cluster procedure involving the Euclidean distances of the pKi values. Nine compounds (compound 13, 14, 16, 19, 22, 23, 28, 29 and 35; Table 1) were selected from the generated cluster tree in such a way to keep them at a maximum possible distance from each other. The test set was employed for external validation of models derived from remaining 25 analogues of the series. The internal consistency, for each of the generated models from training set, was achieved through LOO and L5O procedures. A total number of 481 descriptors, belonging to 0D, 1D and 2D classes, were computed for these compounds utilizing DRAGON software. The descriptors which were poorly correlated with dependent variable, pKi and were intercorrelated among themselves were eliminated initially. The leftover 99 descriptors were collated in a pool and were subjected to CP?MLR. A large number of models were obtained in one, two and three descriptors. In doing so the threshold of filter?3 was successively incremented with increasing number of descriptors (per equation) by considering the r?bar value of the preceding optimum model as the new threshold for next generation. However, the statistical significance was achieved only for 21 models that were obtained in three descriptors. The identified descriptors for them along with their average regression coefficients and the total incidence are given in Table 3. The name of each descriptor is given in the footnote under this Table. Three such models, in the increasing level of significance, are given through Eqs. 1?3.
pKi=42.594(±15.951) PW3–8.231(±1.581) MATS7v+1.463(±0.278) O?058–10.552 n=25, r=0.845, s=0.431, F (3, 21)=17.460, AIC=0.257, FIT=1.541, LOF=0.270, q2 LOO=0.554, q2 L5O=0.563, r2 Test=0.663 (1)
pKi=–0.209(±0.068) RBN–9.081(±1.516) MATS7v+1.433(±0.264) O?058+6.467 n=25, r=0.857, s=0.415, F (3, 21)=19.379, AIC=0.238, FIT=1.710, LOF=0.250, q2 LOO=0.624, q2 L5O=0.625, r2 Test=0.517 (2)
pKi=0.631(±0.129) nR05–7.946(±1.255) MATS7v+1.498(±0.218) O?058+2.900 n=25, r=0.906, s=0.342, F (3, 21) =31.910, AIC=0.161, FIT=2.816, LOF=0.170, q2 LOO=0.732, q2 L5O=0.690, r2 Test=0.660 (3)
where n and F represent, respectively, the number of data points and the F?ratio between the variances of calculated and observed activities. The ±data within the parentheses are the standard errors associated with regression coefficients. FIT is the Kubinyi function[47,48], AIC is the Akaike’s information criterion[49,50] and LOF is the Friedman’s lack of fit factor[51]. The FIT function is closely related to the F?statistic but proved to be a useful parameter for the assessment of the quality of the models. The disadvantage of the F?value is its sensitivity to changes in the number of independent variables, k in the equation that describes the model. The F?value is more sensitive if k is small, whereas it is less sensitive if k is large. The FIT function, on the other hand, is less sensitive to a lower number k but is more sensitive to a larger number k. The best model would yield the highest value for this function. The AIC takes into account the statistical goodness of fit and the number of parameters that have to be estimated to achieve that degree of fit. The model that produces the lower AIC value should be considered potentially the most useful. The LOF factor takes into account the number of terms used in the equation and is not biased, as are the indicator variables, toward large number of parameters. A statistical sound model will generate the lower value of LOF. In a comparative study, where QSAR models are generated from the descriptors belonging to different categories, the FIT function, the AIC criterion and the LOF factor are very important parameters in explaining the best model[52?54]. In all above equations, the F?values remained significant at 99% level [F3,21 (0.01)=4.874] and indices q2 LOO and q2 L5O (>0.5) have accounted for their internal robustness. The r2 Test value, greater than 0.5, specified that the identified test?set is able to validate these models externally. The descriptors RBN, nR05, O?058 and MATS7v involved in these models represent, respectively, number of rotatable bonds, number of five?membered rings, number of doubly bonded oxygen atoms and Moran autocorrelation of lag 7/weighted by atomic van der Waals volume.
| Descriptors | nR05 | MATS7v | O-058 | pKi |
|---|---|---|---|---|
| nR05 | 1.000 | |||
| MATS7v | 0.028 | 1.000 | ||
| O-058 | 0.047 | 0.038 | 1.000 | |
| pKi | 0.179 | 0.304 | 0.195 | 1.000 |
| aMatrix elements are the r2-values | ||||
Table 4: Correlation matrixaamongst the descriptors of eq. 3.
Though all the above models are reliable enough in statistical sense, but the highest variance (r2), in observed activities, is explained only through Eq. 3. The other statistical parameters, s, F, AIC, FIT, LOF and q2 also favoured Eq. 3 as a statistically reliable model and thus retained for further discussion.
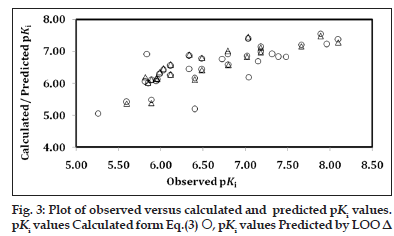
The computed values of descriptors employed in the derivation of Eq. 3 are given in Table 1 for the sake of convenience. That these descriptors have no mutual correlation is shown in Table 4. The descriptor, MATS7v divulged the implication of lag 7, weighted by atomic van der Waals volume. The highest value of descriptor O?058 could be two (Table 1) for the compound under study, advocating the need of both oxygen (O=) atoms. Alternatively, it is essential to have a tartrate core for key binding interaction involving these oxygen atoms through hydrogen bonding with receptor sites. Replacement of any of these oxygen atoms with sulphur (Compounds 33 and 34) and substitution of the nonprime amide with amide isosteres, such as a thiazole or imidazole (Compound 35 and 36), afforded compounds with weaker TACE inhibition and were not advantageous. The loss of activity in these compounds is thought to be caused by the poorer hydrogen?bond acceptor character of sulphur and lack of interactions with the S1 subsite or the face?edge interactions with His415. From Eq. 3, it appeared that the higher values of descriptors nR05 and O?058 and the lower (or more negative) value of MATS7v are conducive in improving the activity of a compound. The calculated and predicted pKis using, respectively, Eq. 3 and LOO procedure, remained in parity with the observed ones (Table 1). The plot, showing the variation of observed versus calculated and predicted pKis is given in fig. 3. Except two ‘outlier’ congeners (Compound 2 and 24), all other compounds have exhibited systematic variation between observed and calculated pKi values, reflecting upon the goodness of fit. Based on Eq. 3, a few potential inhibitors of TACE have been suggested for further exploration. These are given in Table 5 along with descriptors and calculated pKi values. The predicted activities of some of these congeners were much superior to that of highest potent compounds reported in the original series.
| R1 | R2 | nR05 | MATS7v | O-058 | Predicted pKi (M) Eq. 3 |
|---|---|---|---|---|---|
| 2,3-Dihydro-1H-isoindol-2-yl | (4-Benzylthiazol-2-ylmethyl) amino | 2 | −0.101 | 2 | 7.96 |
| 5-Fluoro-2,3-dihydro-1H-isoindol-2-yl | [4-(2-Fluorobenzyl) thiazol-2-ylmethyl] amino | 2 | −0.097 | 2 | 7.93 |
| 5-Chloro-2,3-dihydro-1H-isoindol-2-yl | [4-(2-Chlorobenzyl) thiazol-2-ylmethyl] amino | 2 | −0.060 | 2 | 7.63 |
| 2,3-Dihydro-1H-isoindol-2-yl | [2-(4-Cyclopenta-1,3-dienylthiazol-2-yl) ethyl] amino ethylamino | 3 | −0.035 | 2 | 8.07 |
| 5-Fluoro-2,3-dihydro-1H-isoindol-2-yl | 2-[4-(5-Fluorocyclopenta-1,3-dienyl) thiazol-2-yl] ethylamino | 3 | −0.034 | 2 | 8.06 |
| 5-Chloro-2,3-dihydro-1H-isoindol-2-yl | 2-[4-(5-Chlorocyclopenta-1,3-dienyl) thiazol-2-yl] ethylamino | 3 | −0.029 | 2 | 8.02 |
| For the structure of the basic ring please refer fig. 1a with X=Y=O | |||||
Table 5: Predicted tumour necrosis factor-??converting enzyme inhibition activity of some new tartrate-based analogues.
.
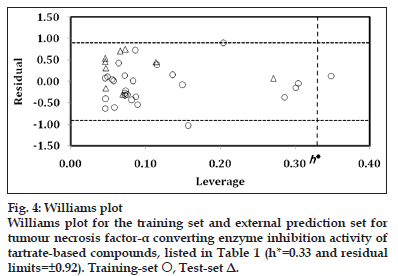
The applicability domain was visualised through the Williams plot (fig. 4) for the highest significant model, obtained for complete data?set as
pKi=0.638(±0.150) nR05–6.269(±1.383) MATS7v+1.540(±0.251) O?058+2.848 n=36, r=0.821, s=0.461, F (3,32)=22.011, q2 LOO=0.586, q2 L5O=0.524 AIC=0.266, FIT=1.467, LOF=0.272 (4)
The limits of normal values for the Y?outliers (response outliers) was set equal to ±2 times the standard deviation and a leverage threshold at h*. For present work, the residual limits and leverage threshold were ±0.92 and 0.33, respectively. From fig. 4, it appeared that compounds 2 and 24 were obvious ‘outliers’ while compound 36 (X?outlier) is a prominent congener to influence the statistics of present series. The residual and leverage of this influential compound were 0.127 and 0.349, respectively. All remaining compounds (training set and test set), present within the square, indicated that the applicability domain is fully justified and the identified model has been evaluated correctly. Furthermore, the derived model matches the high quality parameters with good fitting power and capability of assessing external data.
The present study has, therefore, provided guidelines to develop new tartrate?based analogues which may be potent inhibitors of TNF?α converting enzyme (TACE). The emerged descriptors enlightened the role of Moran autocorrelations pertaining to lag 7, weighted by atomic van der Waals volume, presence of both prime and nonprime amide carbonyl oxygen in the tartrate moiety and occurrence of 5 membered ring bearing substituents at prime and nonprime sites. A few potential novel tartrate?based analogues, as the inhibitors of TNF?α converting enzyme (TACE), have been suggested for further investigation.
Acknowledgements
Author expresses his sincere thanks to the University Grants Commission, New Delhi for sanctioning a research grant to him under the scheme of Emeritus Fellowship and to the Institution for providing necessary facilities to complete this work.
References
- Bradley JR. TNF-mediated inflammatory disease. J Pathol 2008;214:149-60.
- Palladino MA, Bahjat FR, Theodorakis EA, Moldawer LL. Anti-TNF-alpha therapies: The next generation. Nat Rev Drug Discov 2003;2:736-46.
- Newton RC, Decicco CP. Therapeutic potential and strategies for inhibiting tumor necrosis factor -alpha. J Med Chem 1999;42:2295-314.
- Newton RC, Solomon KA, Covington MB, Decicco CP, Haley PJ, Friedman SM, et al. Biology of TACE inhibition. Ann Rheum Dis 2001;60(suppl 3):iii25-32.
- Tracey D, Klareskog L, Sasso EH, Salfeld JG, Tak PP. Tumor necrosis factor antagonist mechanisms of action: A comprehensive review. PharmacolTher 2008;117:244-79.
- Das Gupta S, Murumkar PR, Giridhar R, Yadav MR. Current perspective of TACE inhibitors: A review. Bioorg Med Chem 2009;17:444-59.
- Skotnicki JS, Levin JI. TNF-α converting enzyme (TACE) as a therapeutic target. Annu Rep Med Chem 2003;38:153-62.
- Moss ML, Sklair-Tavron L, Nudelman R. Drug insight: Tumor necrosis factor-converting enzyme as a pharmaceutical target for rheumatoid arthritis. Nat ClinPractRheumatol 2008;4:300-9.
- Black RA, Rauch CT, Kozlosky CJ, Peschon JJ, Slack JL, Wolfson MF, et al. A metalloproteinase disintegrin that releases tumour-necrosis factor-alpha from cells. Nature 1997;385:729-33.
- Moss ML, Jin SL, Milla ME, Bickett DM, Burkhart W, Carter HL, et al. Cloning of a disintegrin metalloproteinase that processes precursor tumour-necrosis factor-alpha. Nature 1997;385:733-6.
- Maskos K, Fernandez-Catalan C, Huber R, Bourenkov GP, Bartunik H, Ellestad GA, et al. Crystal structure of the catalytic domain of human tumor necrosis factor-alpha-converting enzyme. ProcNatlAcadSci USA 1998;95:3408-12.
- Whittaker M, Floyd CD, Brown P, Gearing AJ. Design and therapeutic application of matrix metalloproteinase inhibitors. Chem Rev 1999;99:2735-76.
- Wasserman ZR, Duan JJ, Voss ME, Xue CB, Cherney RJ, Nelson DJ, et al. Identification of a selectivity determinant for inhibition of tumor necrosis factor-alpha converting enzyme by comparative modeling. ChemBiol 2003;10:215-23.
- Huang A, Joseph-McCarthy D, Lovering F, Sun L, Wang W, Xu W, et al. Structure-based design of TACE selective inhibitors: Manipulations in the S1’-S3’ pocket. Bioorg Med Chem 2007;15:6170-81.
- Ott GR, Asakawa N, Lu Z, Anand R, Liu RQ, Covington MB, et al. Potent, exceptionally selective, orally bioavailable inhibitors of TNF-alpha converting enzyme (TACE): Novel 2-substituted-1H-benzo[d] imidazol-1-yl) methyl) benzamide P1’ substituents. Bioorg Med ChemLett 2008;18:1577-82.
- Zhu Z, Mazzola R, Sinning L, McKittrick B, Niu X, Lundell D, et al. Discovery of novel hydroxamates as highly potent tumor necrosis factor-alpha converting enzyme inhibitors: Part I – Discovery of two binding modes. J Med Chem 2008;51:725-36.
- Mazzola RD Jr, Zhu Z, Sinning L, McKittrick B, Lavey B, Spitler J, et al. Discovery of novel hydroxamates as highly potent tumor necrosis factor-alpha converting enzyme inhibitors. Part II: Optimization of the S3’ pocket. Bioorg Med ChemLett 2008;18:5809-14.
- Drummond AH, Beckett P, Brown PD, Bone EA, Davidson AH, Galloway WA, et al. Preclinical and clinical studies of MMP inhibitors in cancer. Ann N Y AcadSci 1999;878:228-35.
- Hutchinson JW, Tierney GM, Parsons SL, Davis TR. Dupuytren’s disease and frozen shoulder induced by treatment with a matrix metalloproteinase inhibitor. J Bone Joint Surg Br 1998;80:907-8.
- Wojtowicz-Praga S, Torri J, Johnson M, Steen V, Marshall J, Ness E, et al. Phase I trial of Marimastat, a novel matrix metalloproteinase inhibitor, administered orally to patients with advanced lung cancer. J ClinOncol 1998;16:2150-6.
- Griffioen AW. AG-3340 (Agouron Pharmaceuticals Inc). IDrugs 2000;3:336-45.
- Levitt NC, Eskens FA, O’Byrne KJ, Propper DJ, Denis LJ, Owen SJ, et al. Phase I and pharmacological study of the oral matrix metalloproteinase inhibitor, MMI270 (CGS27023A), in patients with advanced solid cancer. Clin Cancer Res 2001;7:1912-22.
- Skiles JW, Gonnella NC, Jeng AY. The design, structure, and therapeutic application of matrix metalloproteinase inhibitors. Curr Med Chem 2001;8:425-74.
- Clark IM, Parker AE. Metalloproteinases: Their role in arthritis and potential as therapeutic targets. Expert OpinTher Targets 2003;7:19-34.
- Peterson JT. Matrix metalloproteinase inhibitor development and the remodeling of drug discovery. Heart Fail Rev 2004;9:63-79.
- Levin JI, Chen JM, Laakso LM, Du M, Schmid J, Xu W, et al. Acetylenic TACE inhibitors. Part 3: Thiomorpholine sulfonamide hydroxamates. Bioorg Med ChemLett 2006;16:1605-9.
- Flipo M, Charton J, Hocine A, Dassonneville S, Deprez B, Deprez-Poulain R. Hydroxamates: Relationships between structure and plasma stability. J Med Chem 2009;52:6790-802.
- Rosner KE, Guo Z, Orth P, Shipps GW Jr, Belanger DB, Chan TY, et al. The discovery of novel tartrate -based TNF-alpha converting enzyme (TACE) inhibitors. Bioorg Med ChemLett 2010;20:1189-93.
- Annis DA, Nazef N, Chuang CC, Scott MP, Nash HM. A general technique to rank protein-ligand binding affinities and determine allosteric versus direct binding site competition in compound mixtures. J Am ChemSoc 2004;126:15495-503.
- Annis DA, Shipps GW Jr, Deng Y, Popovici-Müller J, Siddiqui MA, Curran PJ, et al. Method for quantitative protein-ligand affinity measurements in compound mixtures. Anal Chem 2007;79:4538-42.
- Annis DA, Nickbarg E, Yang X, Ziebell MR, Whitehurst CE. Affinity selection-mass spectrometry screening techniques for small molecule drug discovery. CurrOpinChemBiol 2007;11:518-26.
- Guo Z, Orth P, Zhu Z, Mazzola RD, Chan TY, Vaccaro HA, et al. Chemical compounds and pharmaceutical compositions containing them for the treatment of inflammatory disorders. 2005, WO2005121130.
- SYSTAT, version 7.0; SPSS Inc., 444 North Michigan Avenue, Chicago, IL 60611, USA.
- Chemdraw ultra 6.0 and Chem3D ultra, Cambridge Soft Corporation, Cambridge, USA, 2000.
- DRAGON software, version 3.0; by Todeschini R, Consonni V, Mauri A, Pavan M. Milano, Italy, 2003. Available from: http://www. talete.mi.it/dragon.htm [Last accessed on 11 January 2013].
- Prabhakar YS. A combinatorial approach to the variable selection in multiple linear regression: Analysis of Selwood et al. data-set-A case study. QSAR Comb Sci 2003;22:583-95.
- Sharma S, Prabhakar YS, Singh P, Sharma BK. QSAR study about ATP-sensitive potassium channel activation of cromakalim analogues using CP-MLR approach. Eur J Med Chem 2008;43:2354-60.
- Sharma S, Sharma BK, Sharma SK, Singh P, Prabhakar YS. Topological descriptorsin modeling the agonistic activity of human A3 adenosine receptor ligands: The derivatives of 2-chloro-N (6)-substituted-4’-thioadenosine-5’-uronamide. Eur J Med Chem 2009;44:1377-82.
- Sharma BK, Pilania P, Singh P, Prabhakar YS. Combinatorial protocol in multiple linear regression/partial least-squares directed rationale for the caspase-3 inhibition activity of isoquinoline-1,3,4-trione derivatives. SAR QSAR Environ Res 2010;21:169-85.
- Sharma BK, Singh P, Sarbhai K, Prabhakar YS. A quantitative structure-activity relationship study on serotonin 5-HT6 receptor ligands: Indolyl and piperidinylsulphonamides. SAR QSAR Environ Res 2010;21:369-88.
- Sharma BK, Pilania P, Sarbhai K, Singh P, Prabhakar YS. Chemometric descriptors in modeling the carbonic anhydrase inhibition activity of sulfonamide and sulfamate derivatives. Mol Divers 2010;14:371-84.
- Sharma BK, Singh P, Shekhawat M, Sarbhai K, Prabhakar YS. Modelling of serotonin reuptake inhibitory and histamine H3 antagonistic activity of piperazine and diazepane amides: QSAR rationales for co-optimization of the activity profiles. SAR QSAR Environ Res 2011;22:365-83.
- So SS, Karplus M. Three-dimensional quantitative structure-activity relationships from molecular similarity matrices and genetic neural networks. 1. Method and validations. J Med Chem 1997;40:4347-59.
- Prabhakar YS, Solomon VR, Rawal RK, Gupta MK, Katti SB. CP-MLR/PLS directed structure-activity modeling of the HIV-1 RT inhibitory activity of 2,3-diaryl-1,3-thiazolidin-4-ones. QSAR Comb Sci 2004;23:234-44.
- Gramatica P. Principles of QSAR models validation: Internal and external. QSAR Comb Sci 2007;26:694-701.
- Eriksson L, Jaworska J, Worth AP, Cronin MT, McDowell RM, Gramatica P. Methods for reliability and uncertainty assessment and for applicability evaluations of classification- and regression-based QSARs. Environ Health Perspect 2003;111:1361-75.
- Kubinyi H. Variable selection in QSAR studies. I. An evolutionary algorithm. Quant Struct-Act Relat 1994;13:285-94.
- Kubinyi H. Variable selection in QSAR studies. II. A highly efficient combination of systematic search and evolution. Quant Struct-Act Relat 1994;13:393-401.
- Akaike H. Information theory and an extension of the minimum likelihood principle. In: Petrov BN, Csaki F, editors. Second International Symposium on Information Theory. Budapest: AkademiaiKiado; 1973. p. 267-81.
- Akaike H. A new look at the statistical identification model. IEEE Trans Automat Contr 1974;AC-19:716-23.
- Friedman J. Multivariate Adaptive Regression Splines. Technical Report No. 102. Laboratory for computational statistics. Stanford: Stanford University; November 1988.
- González MP, Caballero J, Tundidor-Camba A, Helguera AM, Fernández M. Modeling of farnesyltransferase inhibition by some thiol and non-thiolpeptidomimetic inhibitors using genetic neural networks and RDF approaches. Bioorg Med Chem 2006;14:200-13.
- Saíz-Urra L, González MP, Teijeira M. QSAR studies about cytotoxicity of benzophenazines with dual inhibition toward both topoisomerases I and II: 3D-MoRSE descriptors and statistical considerations about variable selection. Bioorg Med Chem 2006;14:7347-58.
- Saíz-Urra L, González MP, Teijeira M. 2D-autocorrelation descriptors for predicting cytotoxicity of naphthoquinone ester derivatives against oral human epidermoid carcinoma. Bioorg Med Chem 2007;15:3565-71.