- *Corresponding Author:
- Rathi P.B
Shri Bhagwan College of Pharmacy, N-6, CIDCO, Auranagabad-431 003, India
E-mail: pavanbrathi@gmail.com
| Date of Submission | 19 January 2011 |
| Date of Revision | 21 October 2011 |
| Date of Acceptance | 31 October 2011 |
| Indian J Pharm Sci, 2011, 73 (6): 670-674 |
Abstract
Extended Hildebrand solubility approach is used to estimate the solubility of satranidazole in binary solvent systems. The solubility of satranidazole in various propylene glycol-water mixtures was analyzed in terms of solute-solvent interactions using a modified version of Hildebrand-Scatchard treatment for regular solutions. The solubility equation employs term interaction energy (W) to replace the geometric mean (δ1δ2), where δ1 and δ2 are the cohesive energy densities for the solvent and solute, respectively. The new equation provides an accurate prediction of solubility once the interaction energy, W, is obtained. In this case, the energy term is regressed against a polynomial in δ1 of the binary mixture. A quartic expression of W in terms of solvent solubility parameter was found for predicting the solubility of satranidazole in propylene glycol-water mixtures. The expression yields an error in mole fraction solubility of ~3.74%, a value approximating that of the experimentally determined solubility. The method has potential usefulness in preformulation and formulation studies during which solubility prediction is important for drug design.
Keywords
Extended Hildebrand solubility approach, propylene glycol, regular solution theory, satranidazole, solubility parameter
Solubility data on drugs and pharmaceutical adjuncts in mixed solvents have wide applications in the drug sciences. Knowledge of interaction forces between solutes and solvents are of considerable theoretical and practical interest throughout the physical and biological sciences [1]. The theory of solution is one of the most challenging branches of physical chemistry. The Hildebrand-Scatchard theory of regular solution is the pioneer approach in this field, used to estimate solubility only for relatively non-polar drugs in non-polar solvents [2]. An irregular solution is one in which self-association of solute or solvent, solvation of the solute by the solvent molecules, or complexation of two or more solute species are involved [3]. Polar systems exhibit irregular solution behaviour and are commonly encountered in pharmacy. Extended Hildebrand solubility approach (EHSA), modification of the Hildebrand-Scatchard equation, permits calculation of the solubility of polar and non-polar solutes in solvents ranging from non-polar hydrocarbons to highly polar solvents such as water, ethanol, and glycols [4]. The solubility parameters of solute and solvent were introduced to explain the behaviour of regular and irregular solutions [5]. The EHSA has been developed to reproduce the solubility of drugs and other solids in the binary solvent systems [6].
The Hildebrand-Scatchard equation for the solubility of crystalline solids in a regular solution may be written as [7],
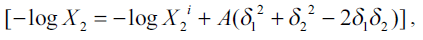 (1a)
(1a)
![]() (1b)
(1b)
The Extended Hildebrand equation for the solubility of solids in an irregular solution may be written as [8],
![]() (2)
(2)
From the geometric mean:
![]() (3a)
(3a)
In pharmaceutical solutions, the geometric mean of δ1 and δ2 is too restrictive and ordinarily provides a poor fit to experimental data in irregular solutions. The assumption that the geometric mean of two geometric parameters δ1δ2 (Eqn. 1) can be replaced by a less restrictive term W (Eqn. 2), interaction energy parameter, which is allowed to take on values as required to yield correct mole fraction solubilities, X2 as [9],
![]() (3b)
(3b)
where, K is the proportionality factor relating W to the geometric mean of solubility parameter.
In Eqn. 1 and Eqn. 2, X2 and X2 i are the mole fraction solubility and ideal mole fraction solubility of the solute respectively. The terms δ1 and δ2 are the solubility parameters for the solvent and solute respectively. The geometric mean, δ1 δ2, provides a reasonable estimate of solvent-solute interaction in regular (ordinarily non-polar) mixtures, whereas W or K δ1 δ2 is required to express solubility’s in non-regular systems (irregular solutions) of drugs in associating mixed solvents.
The term negative logarithm of the ideal solubility (–log X2 i) can be taken as [10],
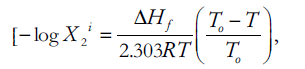 (4)
(4)
Where, ΔHf is heat of fusion of the crystalline drug molecule, T0 is the melting point of solute in absolute degrees.
The term A in equations 1 and 2 is defined as[11],
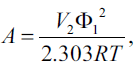 (5)
(5)
Where, V2 is the molar volume of the solute as a hypothetical supercooled liquid at solution temperature, R is the universal gas constant, T is the absolute temperature, 298.2°K, of the experiment and Φ1, the volume fraction of the solvent, is [12],
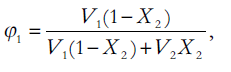 (6)
(6)
Where, V1 is the molar volume of the solvent at 25°. The term logarithmic solute activity coefficient (log γ2) from Eqn. 2 and Eqn. 5 can be written as [13],
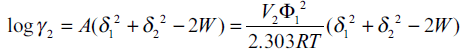 (7)
(7)
A better approach is not to restrict the interaction term W to a geometric mean but evaluate it experimentally from the solubility of the solute in various solvent concentrations in a binary mixture employing Eqn. 2. An empirical equation for W as a function of solubility parameters of the solvent mixture remains to be discovered. Then, backcalculating W and substituting into Eqn. 2 permit the mole fraction solubility of a drug (solute) to be predicted in essentially any solvent mixture. Therefore, the present investigation pertains to the utility of EHSA in relation to the satranidazole solubility in propylene glycol (PG)-water binary solvent mixtures.
Satranidazole, obtained as gift sample from Alkem Laboratories Ltd., Baddi, India, was purified by recrystallization from acetone. Propylene glycol and acetone were purchased from ICPA Laboratories; Ankleshwar, India and Qualigens Fine Chemicals, Mumbai, India respectively. Throughout the study freshly prepared double distilled water was used for experimental purpose. All chemicals and reagents used in the study were of analytical grade and used as such. Double beam UV/Vis spectrophotometer, Shimadzu model 1601 with spectral bandwidth of 2 nm, wavelength accuracy ±0.5 nm and a pair of 10 mm matched quartz cells was used to measure absorbance of the resulting solutions. Citizen balance, CX-100, was used for weighing of Satranidazole. Differential Scanning Calorimeter, Shimadzu TA-60 WS, was used for determination of melting point and heat of fusion of satranidazole.
The solubility of satranidazole was determined in binary solvent mixtures of PG and water. Double distilled water was used to prepare mixtures with PG in concentrations of 0-100% by volume of PG. About 10 ml of PG, water, or binary solvent blends were introduced into screw-capped vials containing an excess amount of satranidazole. After being sealed with several turns of electrical tape, the vials were submerged in water at 25±0.4° and were shaken at 150 rpm for 24 h in a constanttemperature bath. Preliminary studies showed that this time period was sufficient to ensure saturation at 25°[14].
After equilibration, the solutions were microfiltered (0.45 μm) and the filtrate was then diluted with double distilled water to carry out the spectrophotometric determination at the maximum wavelength of absorption of the satranidazole (λmax-319.80 nm). The solubility of the satranidazole was determined at least three times for this solvent mixture, and the average value was taken. The densities of the solvent mixtures and the filtrates of saturated solutions of satranidazole were determined in triplicate at 25±0.4° using 10-ml specific gravity bottle. Once the densities of solutions are known, the solubilities can be expressed in mole fraction scale.
The solubility parameters of the solvents were obtained from the literature [15,16]. The solubility parameter of satranidazole was calculated previously by Fedor’s group contribution method [17,18], which was confirmed by solubility analysis in dioxane-water blend.
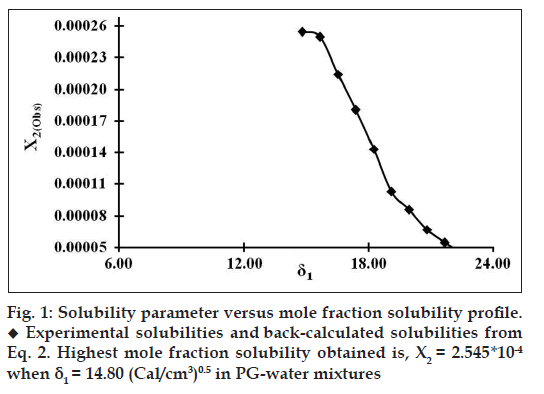
The thermogram of satranidazole was obtained with a differential scanning calorimeter[19]. The melting point and heat of fusion were measured. Sample of 8.8 mg in perforated pan was heated at a rate of 15°/min under nitrogen purge. The temperature range studied was 25-225°. The molar enthalpy of fusion of satranidazole was 112.30 J/g (7763.838 cal/mol) and the temperature of fusion is 461.83°K. Neither decomposition nor polymorphic change was observed at the experimental temperature range. The ideal mole fraction solubility of satranidazole was calculated from these values (–logX2i = 1.61). The mole fraction solubilities of satranidazole at 25±0.4° in PG-water binary mixtures which cover a large range of the solubility parameter scale, from 14.80 to 23.40 (Cal/cm3)0.5, are listed in Table 1. The experimental mole fraction solubility of satranidazole at 25±0.4° in PG-water mixtures is plotted in fig. 1 versus the solubility parameter, δ1, of the various mixed solvent systems. The mole fraction solubility of satranidazole (δ2=14.80) in PG (δ1=14.80), water (δ1=23.4), and in the mixture of the two solvents is represented by the solid circles in fig. 1. The maximum solubility of satranidazole in the mixture is X2=0.0002545 mol/l and occurs at δ1=14.80. This value is well below the ideal solubility, X2i =0.0245614 mol/l, as predicted from regular solution theory. The discrepancy between the results using the original Hildebrand-Scatchard equation and experimental points demonstrates that Eqn. 1a and Eqn. 1b cannot be used to predict drug solubility in PG-water binary solvent systems. This behavior has been dealt with the theoretical replacement of mean geometric solubility parameters (δ1δ2) term with the interaction energy term (W).
| PG-Water (%v/v) | Solubility | d1 | V1 | Density of | Mol. Wt | X2(obs) | W(obs) |
|---|---|---|---|---|---|---|---|
| (g/ml) | (Cal/cm3)0.5 | blend | of blend | ||||
| 0:100 | 0.0005025 | 23.40 | 18.00 | 0.9980 | 18.00 | 3.1350E-05 | 330.26 |
| 10:90 | 0.0005350 | 22.54 | 23.56 | 1.0018 | 23.81 | 4.3980E-05 | 310.93 |
| 20:80 | 0.0005350 | 21.68 | 29.12 | 1.0056 | 29.62 | 5.4505E-05 | 292.19 |
| 30:70 | 0.0005495 | 20.82 | 34.68 | 1.0094 | 35.43 | 6.6711E-05 | 274.17 |
| 40:60 | 0.0006073 | 19.96 | 40.24 | 1.0132 | 41.24 | 8.5499E-05 | 256.95 |
| 50:50 | 0.0006435 | 19.10 | 45.80 | 1.0170 | 47.05 | 1.0298E-04 | 240.38 |
| 60:40 | 0.0007990 | 18.24 | 51.36 | 1.0208 | 52.86 | 1.4313E-04 | 224.74 |
| 70:30 | 0.0009111 | 17.38 | 56.92 | 1.0246 | 58.67 | 1.8048E-04 | 209.71 |
| 80:20 | 0.0009870 | 16.52 | 62.48 | 1.0284 | 64.48 | 2.1410E-04 | 195.35 |
| 90:10 | 0.0010593 | 15.66 | 68.04 | 1.0322 | 70.29 | 2.4957E-04 | 181.71 |
| 100:0 | 0.0010015 | 14.80 | 73.60 | 1.0360 | 76.10 | 2.5450E-04 | 168.63 |
δ1= Solubility parameter of solvent blend, V1= molar volume of the solvent blend, and W is calculated from Eqn. 2
Table 1: Mole Fraction Solubility Of Satranidazole
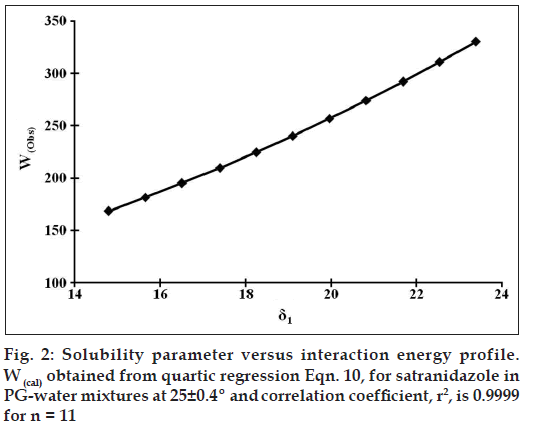
Eqn. 2, differs from Eqn. 1, in that the geometric mean is not used, hence provides an accurate prediction of solubility once W is obtained. Although W presently cannot be estimated based on fundamental physicochemical properties of the solute and solvent, W may be regressed against a polynomial in δ1 of the PG-water binary solvent mixtures (fig. 2). The following quadratic, cubic, and quartic equations were obtained using the experimental solubility data for satranidazole in PG-water mixtures: Wcal = 59.67364 + 0.15209 δ1 + 0.48767 δ1 2 (n = 11, R2 = 0.99999816)--- (8), Wcal = 39.74407 + 3.36052 δ1 + 0.31765 δ12 + 0.00297 δ13 (n = 11, R2 = 0.99999892)- - -(9), Wcal = -132.17742 + 40.31464 δ1 – 2.63481 δ1 2 + 0.10690 δ1 3 - 0.00136 δ1 4 (n = 11, R2 = 0.99999971)---(10).
The W values calculated using these expressions compared favorably with the original W values computed using Eqn. 2. The solid line plotted in fig. 2 was obtained employing the quartic expression (Eqn. 10). The calculated solubility curve fits the experimental data points quite well (figs. 1 and 3), predicting the solubility of satranidazole in PG-water mixtures at most points within an error of ~3.74%, approximating the error in experimentally determined solubility values. These polynomials are used successfully for the calculation of W, at any value of solubility parameter (δ1), which was then subsequently employed to calculate mole fraction solubility of solute (X2cal) in a solvent blend using backward regression. Representative data along with validation parameters are summarized in Table 1. Wcal values are indicating the significant interaction of satranidazole and solvent molecules at the peak of solubility profile.
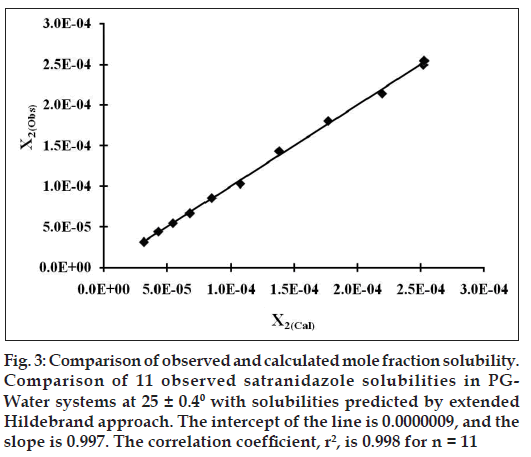
Figure 3: Comparison of observed and calculated mole fraction solubility. Comparison of 11 observed satranidazole solubilities in PG Water systems at 25 ± 0.40 with solubilities predicted by extended Hildebrand approach. The intercept of the line is 0.0000009, and the slope is 0.997. The correlation coefficient, r2, is 0.998 for n = 11
Validation of Eqn. 10 was done by comparing experimentally obtained and calculated values of mole fraction solubility by estimating residuals and percent difference (Table 2). The predictive capability of the model for satranidazole is represented in fig. 3, which indicates a very high degree of correlation coefficient (R2) 0.998 and negligible intercept equal to zero.
| W(obs) | W(cal) | X2(obs) | X2(cal) | logγ2/A(obs) | logγ2/A(cal) | Residual | Percent difference |
|---|---|---|---|---|---|---|---|
| 330.263794 | 330.277402 | 3.1350E-05 | 3.1691E-05 | 16.764513 | 16.737296 | -1.0877E-02 | -1.1 |
| 310.934967 | 310.905039 | 4.3980E-05 | 4.2946E-05 | 15.913766 | 15.973622 | 2.3510E-02 | 2.4 |
| 292.190240 | 292.192184 | 5.4505E-05 | 5.4589E-05 | 15.374020 | 15.370132 | -1.5463E-03 | -0.2 |
| 274.169268 | 274.190019 | 6.6711E-05 | 6.7820E-05 | 14.865963 | 14.824463 | -1.6631E-02 | -1.7 |
| 256.945357 | 256.931866 | 8.5499E-05 | 8.4587E-05 | 14.242986 | 14.269967 | 1.0666E-02 | 1.1 |
| 240.383226 | 240.433191 | 1.0298E-04 | 1.0715E-04 | 13.775647 | 13.675717 | -4.0511E-02 | -4.1 |
| 224.739543 | 224.691600 | 1.4313E-04 | 1.3778E-04 | 12.950614 | 13.046501 | 3.7379E-02 | 3.7 |
| 209.713663 | 209.686837 | 1.8048E-04 | 1.7667E-04 | 12.369174 | 12.422825 | 2.1086E-02 | 2.1 |
| 195.350960 | 195.380792 | 2.1410E-04 | 2.1923E-04 | 11.940579 | 11.880916 | -2.3980E-02 | -2.4 |
| 181.705894 | 181.717492 | 2.4957E-04 | 2.5188E-04 | 11.555913 | 11.532715 | -9.2549E-03 | -0.9 |
| 168.633292 | 168.623108 | 2.5450E-04 | 2.5245E-04 | 11.505517 | 11.525884 | 8.0566E-03 | 0.8 |
Wcal obtained from quartic Eqn. 10, for Satranidazole in PG-water mixtures at 25 ± 0.4°. Residuals can also be obtained from, [(X2(obs)-X2(cal))/ X2(obs)]
Table 2: Experimental And Calculated Mole Fraction Solubilities.
EHSA employs a power series (quartic) equation in δ1 to back-calculate W, which reproduces the solubility of satranidazole in PG-water mixtures within the accuracy ordinarily achieved in such experimental solubility results. On the basis of validation parameters, it can be expressed that the behavior of irregular solution can be quantified more precisely using EHSA. The procedure can be explored further to predict the solubility of satranidazole in any other binary solvent mixtures. Simultaneously, this tool may become useful in optimization problems of clear solution formulations. Thus the method has potential usefulness in preformulation and formulation studies during which solubility prediction is important for drug design.
Acknowledgements
Author wishes to express his gratitude to M/S Alkem Laboratories Limited, Baddi, India for providing gift sample of Satranidazole.
References
- Martin A, Newburger J, Adjei A. Extended Hildebrand solubility approach: solubility of theophylline in polar binary solvents. J Pharm Sci 1980;69:487-91.
- Wu PL, Martin A. Extended Hildebrand solubility approach: hydroxybenzoic acid in mixtures of dioxane and water. J Pharm Sci 1983;72:587-92.
- Thimmasetty J, Subramanyam CVS, Vishwanath BA, SateshSabu PR. Solubility Parameter Estimation of Celecoxib by Current Methods. Asian J Res Chem 2009;2:188-95.
- Subramanyam CV, Sreenivasa RM, Venkata RJ, Gundu RP. Irregular solution behaviour of paracetamol in binary solvents. Int J Pharm 1992;78:17-24.
- Babu PR, Subrahmanyam CV, Thimmasetty J, Manavalan RValliappan K. Extended Hansen?s Solubility Approach: Meloxicam in Individual Solvents. Pak J Pharm Sci 2007;20:311-6.
- Martin A, Carstensen J. Extended solubility approach: solubility parameters for crystalline compounds. J Pharm Sci 1981;70:170-2.
- Martin A, Wu PL, Velasquez T. Extended hildebrand solubility approach: sulfonamides in binary and ternary solvents. J Pharm Sci 1985;74:277-82.
- Martin A, Miralles MJ. Extended Hildebrand solubility approach: solubility of tolbutamide, acetohexamide and sulfisomidine in binary solvent mixtures. J Pharm Sci 2006;71:439-42.
- Mourya VK, Yadav SK, Saini TR. Solubility Studies of Metronidazole in Binary Solvent Blends. Indian J Pharm Sci 1997;59:200-2.
- Martin A, Wu PL, Adjei A, Mehdizadeh M, James KC, Metzler C. Extended Hildebrand solubility approach: testosterone and testosterone propionate in binary solvents. J Pharm Sci 1982;71:1334-40.
- Beerbower A, Wu PL, Martin A. Expanded solubility parameter approach i: napthalene and benzoic acid in individual solvents. J Pharm Sci 1984;73:179-88.
- Jouyban-Gharamaleki A, Acree WE Jr. Comments concerning: solubility prediction of caffeine in aqueous n, n-dimethyl formamide mixtures using the extended Hildebrand solubility approach. Int J Pharm 1997;156:239-44.
- Martin A, WU PL, Liron Z, Cohen S. Dependence of solute solubility parameters on solvent polarity. J Pharm Sci 1985;74:638-42.
- Rathi PB. Determination and evaluation of solubility parameter of satranidazole using dioxane-water system. Indian J Pharm Sci 2010;72:671-4.
- Adjei A, Newburger J, Martin A. Extended Hildebrand approach: solubility of caffeine in dioxane-water mixtures. J Pharm Sci 1980;69:659-61.
- Patrick JS. Martin?s Physical Pharmacy and Pharmaceutical Sciences. 5th ed. Philadelphia: Lippincott Williams and Wilkins; 2006. p. 245-46 and p. 595-96.
- Barton AF. CRC Handbook of Solubility Parameters and other Cohesion Parameters. 2nd ed. New York: CRC Press; 1983. p. 7-59 and p. 157-85.
- Greenhalgh DJ, Williams AC, Timmins P, York P. Solubility Parameters as Predictors of Miscibility in Solid Dispersions. J Pharm Sci 1999;88:1182-90.
- Jouyban-Gharamaleki A, Romero S, Bustamante P, Clark BJ. Multiple solubility maxima of oxolinic acid in mixed solvents and a new extension of hildebrand solubility approach. Chem Pharm Bull 2000;48:175-8.